Question

【题目】如图，在四边形ABCD中，对角线AC，BD交于点E，∠BAC＝90°，∠CED＝45°，BE＝2DE＝2，CD＝．

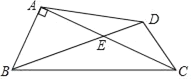
（1）求AB的长；

（2）求AC的长．

Answer 1

【答案】（1）；（2）

【解析】

（1）根据等腰直角三角形的判定和性质即可得到结论；

（2）过点D作DH⊥AC，根据等腰直角三角形的性质和勾股定理分别求出EH和CH即可．

解：（1）∵∠BAC＝90°，∠CED＝45°，

∴∠AEB＝∠CED＝45°，

∴△ABE是等腰直角三角形，

∵BE＝2，

∴AB＝BE＝；

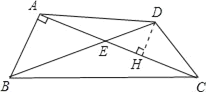
（2）过点D作DH⊥AC交AC于H，

∵∠CED＝45°，DH⊥EC，DE＝，

∴EH＝DH＝DE＝，

又∵CD＝，

∴CH＝＝＝，

∵AE＝AB＝，

∴AC＝CH+EH+AE＝.