题目内容
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的一个动点,作直线
上的一个动点,作直线![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,设点
,设点![]() 、
、![]() 在直线
在直线![]() 上,则
上,则![]() 为( )
为( )
A.2B.![]() C.3D.
C.3D.![]()
【答案】B
【解析】
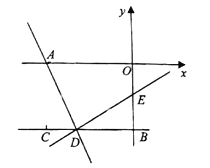
由点的坐标可知四边形OACB是矩形,由DE⊥AD,AD=DE,可得△ACD≌△DBE,从而得到DB=AC=2,CD=BE=1,求出点D、E的坐标,代入y=kx+b,可求出k的值.
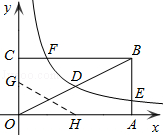
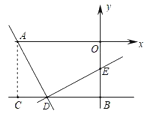
解:连接AC,
∵A(3,0),B(0,2),C(3,2),
∴OACB是矩形,
∴AC=OB=2,OA=BC=3,∠ACD=∠DBE=90°,
又∵DE⊥AD,
∴∠ADE=90°,
∴∠ADC+∠DAC=∠ADC+∠EDB=90°,
∴∠DAC=∠EDB,
∵AD=DE,
∴△ACD≌△DBE(AAS),
∴DB=AC=2,CD=BE=32=1,
∴D(2,2),E(0,1),
将D,E坐标代入y=kx+b得:![]() ,
,
解得: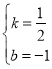 ,
,
故选:B.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
【题目】某个体小服装店主准备在夏季来临前,购进甲、乙两种T恤.两种T恤的相关信息如表:
品牌 | 甲 | 乙 |
进价(元/件) | 45 | 80 |
售价(元/件) | 75 | 120 |
根据上述信息,该店决定用不少于6198元,但不超过6296元的资金购进这两种T恤共100件请解答下列问题:
(1)该店有哪几种进货方案?
(2)该店按哪种方案进货所获利润最大,最大利润是多少?