题目内容
【题目】在圆O中,C是弦AB上的一点,联结OC并延长,交劣弧AB于点D,联结AO、BO、
AD、BD.已知圆O的半径长为5,弦AB的长为8.
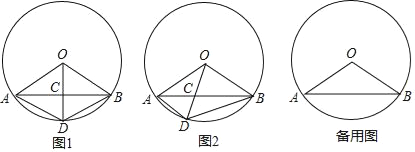
(1)如图1,当点D是弧AB的中点时,求CD的长;
(2)如图2,设AC=x,![]() =y,求y关于x的函数解析式并写出定义域;
=y,求y关于x的函数解析式并写出定义域;
(3)若四边形AOBD是梯形,求AD的长.
【答案】(1)2;(2)y=![]() (0<x<8);(3)AD=
(0<x<8);(3)AD=![]() 或6.
或6.
【解析】
(1)根据垂径定理和勾股定理可求出OC的长.
(2)分别作OH⊥AB,DG⊥AB,用含x的代数式表示△ACO和△BOD的面积,便可得出函数解析式.
(3)分OB∥AD和OA∥BD两种情况讨论.
解:(1)∵OD过圆心,点D是弧AB的中点,AB=8,
∴OD⊥AB,AC=![]() AB=4,
AB=4,
在Rt△AOC中,∵∠ACO=90°,AO=5,
∴CO=![]() =3,
=3,
∴OD=5,
∴CD=OD﹣OC=2;
(2)如图2,过点O作OH⊥AB,垂足为点H,
则由(1)可得AH=4,OH=3,
∵AC=x,
∴CH=|x﹣4|,
在Rt△HOC中,∵∠CHO=90°,AO=5,
∴CO=![]() =
=![]() =
=![]() ,
,
∴CD=OD﹣OC=5﹣![]() ,
,
过点DG⊥AB于G,
∵OH⊥AB,
∴DG∥OH,
∴△OCH∽△DCG,
∴![]() ,
,
∴DG=![]() =
=![]() ,
,
∴S△ACO=![]() AC×OH=
AC×OH=![]() x×3=
x×3=![]() x,
x,
S△BOD=![]() BC(OH+DG)=
BC(OH+DG)=![]() (8﹣x)×(3+
(8﹣x)×(3+![]() )=
)=![]() (8﹣x)×
(8﹣x)×![]()
∴y=![]() =
= =
=![]() (0<x<8)
(0<x<8)
(3)①当OB∥AD时,如图3,
过点A作AE⊥OB交BO延长线于点E,过点O作OF⊥AD,垂足为点F,
则OF=AE,
∴S=![]() ABOH=
ABOH=![]() OBAE,
OBAE,
AE=![]() =
=![]() =OF,
=OF,
在Rt△AOF中,∠AFO=90°,AO=5,
∴AF=![]() =
=![]()
∵OF过圆心,OF⊥AD,
∴AD=2AF=![]() .
.
②当OA∥BD时,如图4,过点B作BM⊥OA交AO延长线于点M,过点D作DG⊥AO,垂足为点G,
则由①的方法可得DG=BM=![]() ,
,
在Rt△GOD中,∠DGO=90°,DO=5,
∴GO=![]() =
=![]() ,AG=AO﹣GO=
,AG=AO﹣GO=![]() ,
,
在Rt△GAD中,∠DGA=90°,
∴AD=![]() =6
=6
综上得AD=![]() 或6.
或6.



故答案为:(1)2;(2)y=![]() (0<x<8);(3)AD=
(0<x<8);(3)AD=![]() 或6.
或6.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案