Question

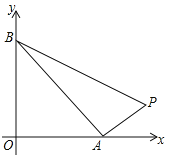
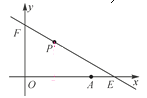
【题目】如图，在平面直角坐标系中，菱形的顶点与原点重合，点在轴的

正半轴上，点在反比例函数的图象上，点的坐标为．

求的值．

若将菱形向右平移，使点落在反比例函数的图象上，求菱形平移的距离．

怎样平移可以使点、同时落在第一象限的曲线上？

Answer 1

【答案】（1）；（2）菱形向右平移的距离为：；（3）菱形向右平移个单位，下移个单位，点、同时落在第一象限的曲线上．

【解析】

①作，轴于点，可得出A的坐标（4,8），根据反比例上的点横纵坐标之积=k，即可得出k；

②可以先求出点的纵坐标为，再求出= ，相减后即可求出；

③先设图象向右平移个单位，向下平移个单位，得出B,D坐标，带入解析式即可得出答案.

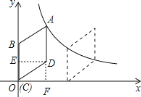
解：作，轴于点，

，

∵点的坐标为，

∴，，

∴，

∴，

∴点坐标为：，

∴，

∴；

∵将菱形向右平移，使点落在反比例函数的图象上，

∴，，

∴点的纵坐标为，

∴，

，

∴，

∴，

∴菱形向右平移的距离为：；图象向右平移个单位，向下平移个单位，

，在图象上，

，

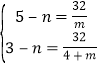解得．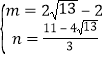

则菱形向右平移个单位，下移个单位，点、同时落在第一象限的曲线上．