题目内容
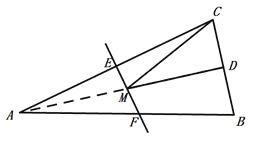
【题目】如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 （ ）
A.8B.10C.12D.14
【答案】D
【解析】
连接AD，根据等腰三角形的性质以及垂直平分线的性质结合三角形的面积公式求出AD的长，再根据垂直平分线的性质知点C关于直线EF的对称点为点A，故A、M、D共线时△CDM的周长的最小，由此即可得出结论．
连接AD，
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴
，
解得AD=12，
∵EF是线段AC的垂直平分线，
∴点C关于直线EF的对称点为点A，
∴AD的长为CM+MD的最小值，
∴△CDM的周长最短
故选：D
练习册系列答案
小学夺冠AB卷系列答案
相关题目
