题目内容
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球，这些球除颜色外其他都相同．
（1）求从袋中摸出一个球是黄球的概率；
（2）求从袋中摸出一个球不是红球的概率；
（3）现在从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后，若从袋中摸出一个球是黄球的概率为
，则取出了多少个黑球？
【答案】（1）
；（2）
；（3）取出了11个黑球
【解析】
（1）用黄球的个数除以球的总个数即可得；
（2）用不是红球的个数，即黄球和黑球的个数除以总个数即可得；
（3）设取出了x个黑球，用变化后黄球的数量÷总数量=摸出一个球是黄球的概率列出方程，解之可得．
（1）因为共有5+13+22=40个小球，
所以从袋中摸出一个球是黄球的概率为
=
；
（2）从袋中摸出一个球不是红球的概率为
=
；
（3）设取出了x个黑球，
根据题意，得：
=
，
解得：x=11，
答：取出了11个黑球．
练习册系列答案
相关题目
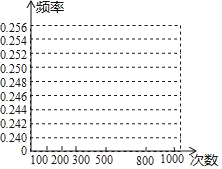
【题目】盒中有若干枚黑棋和白棋，这些棋除颜色外无其他差别，现让学生进行摸棋试验：每次摸出一枚棋，记录颜色后放回摇匀，重复进行这样的试验得到以下数据：
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | b | 201 | 250 |
摸到黑棋的频率 | 0.240 | a | 0.253 | 0.248 | 0.251 | 0.250 |
（1）填空：a= ，b= ；
（2）在图中，画出摸到黑棋的折线统计图；
（3）随机摸一次，估计摸到黑棋的概率．（精确到0.01）
