题目内容
【题目】△ABC中,BC=8,以AC为边向外作等边△ACD.
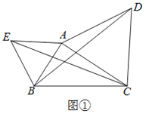
(1)如图①,△ABE是等边三角形,若AC=6,∠ACB=30°,求CE的长;
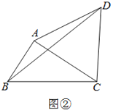
(2)如图②,若∠ABC=60°,AB=4,求BD的长.
【答案】(1)10;(2)![]()
【解析】
(1)根据等边三角形的性质及等式的性质求得![]() ,然后利用边角边定理证明
,然后利用边角边定理证明![]() ,从而求得
,从而求得![]() ,然后判定
,然后判定![]() 为直角三角形,利用勾股定理求BD的长,使问题得解;
为直角三角形,利用勾股定理求BD的长,使问题得解;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,求得
,求得![]() 是等边三角形,
是等边三角形,![]() 是等腰三角形,从而求得
是等腰三角形,从而求得![]() ,∠BAC=90° ,然后利用勾股定理求解.
,∠BAC=90° ,然后利用勾股定理求解.
(1)∵![]() 和
和![]() 都是等边三角形.
都是等边三角形.
∴![]() ,
,![]()
![]()
∴![]()
∴![]()
∴![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]() ,
,![]() 为直角三角形.
为直角三角形.
∴![]()
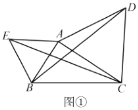
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵BC=8,∴BE=CE=AB=4
又∵∠ABC=60°
∴![]() 是等边三角形,
是等边三角形,![]() 是等腰三角形,
是等腰三角形,
∴∠AEB=2∠ECA=60°,即∠ECA=30°
由△ADC为等边三角形,可知∠ACD=60°
∴![]() ,∠BAC=90°
,∠BAC=90°
∴在Rt△ABC中,![]()
∴在Rt△BCD中,![]()


练习册系列答案
相关题目