Question

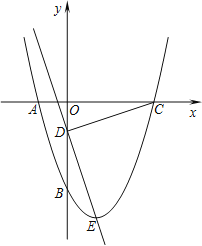
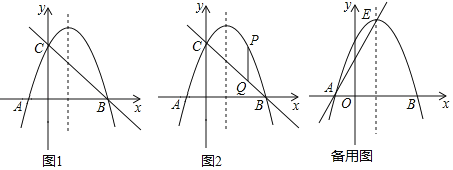
【题目】如图1，抛物线y＝﹣x2+2x+3的图象与x轴交于点A、B，与y轴交于点C，连接BC．

（1）求直线BC的解析式；

（2）如图2，点P是抛物线在第一象限内的一点，作PQ∥y轴交BC于Q，当线段PQ的长度最大时，在x轴上找一点M，使PM+CM的值最小，求PM+CM的最小值；

（3）抛物线的顶点为点E，连接AE，在抛物线上是否存在一点N，使得直线AN与直线AE的夹角为45度，若存在请直接写出满足条件的点N的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）y＝﹣x+3；（2）；（3）点N的坐标为：（﹣，）．

【解析】

（1）抛物线x轴交于点A、B，与y轴交于点C，则点A、B、C的坐标分别为：（-1，0）、（3，0）、（0，3），即可求解；
（2）取点C关于x轴的对称点C′（0，-3），连接PC′交x轴于点M，则点M为所求点，此时PM+CM的最小，即可求解；
（3）设GM=AG=x，则GE=2x，AE=AG+EG=3x=，解得：x=，HM2=AH2-OM2=（x）24=，故HM=，则点H（1，），将点A、H代入一次函数表达式并解得：直线AH（N）的表达式为：y=x+，即可求解．

解：（1）抛物线y＝﹣x2+2x+3，抛物线x轴交于点A、B，与y轴交于点C，

则点A、B、C的坐标分别为：（﹣1，0）、（3，0）、（0，3），

∴将点B、C的坐标代入一次函数表达式：y＝kx+b并解得：

直线BC的表达式为：y＝﹣x+3；

（2）设点P（x，﹣x2+2x+3），则点Q（x，﹣x+3），

PQ＝﹣x2+2x+3+x﹣3＝﹣x2+3x，

当x＝时，PQ有最大值，此时点P（，）；

取点C关于x轴的对称点C′（0，﹣3），连接PC′交x轴于点M，则点M为所求点，此时PM+CM的最小，

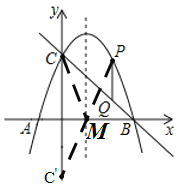
∴PM+CM的最小值＝PC′=；

（3）如图，设直线AN交对称轴于点H，故点H作HG⊥AE于点G，对称轴交x轴于点M，

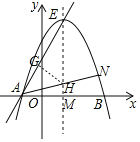
tan∠AEM＝，设GM＝AG＝x，则GE＝2x，

AE＝AG+EG＝3x＝，解得：x＝，

HM2＝AH2﹣OM2＝（）2﹣4＝，

∴HM＝，则点H（1，），

将点A、H代入一次函数表达式并解得：

直线AH（N）的表达式为：；

联立直线BC和直线AH，则：

，

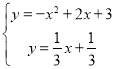解得：x＝或﹣1（舍去﹣1），

故点N的坐标为：（﹣，）．