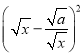Question

【题目】（发现问题）爱好数学的小明在做作业时碰到这样的一道题目：

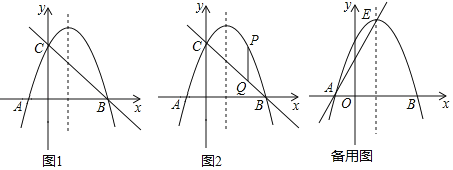
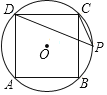
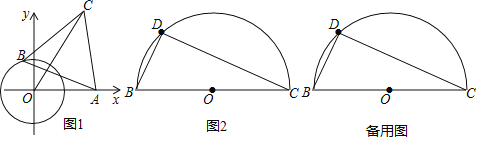
如图1，点O为坐标原点，⊙O的半径为1，点A（2，0）．动点B在⊙O上，连结AB，作等边△ABC（A，B，C为顺时针顺序），求OC的最大值．

（解决问题）小明经过多次的尝试与探索，终于得到解题思路：在图①中，连接OB，以OB为边在OB的左侧作等边三角形BOE，连接AE．

（1）请你找出图中与OC相等的线段，并说明理由；

（2）请直接写出线段OC的最大值．

（迁移拓展）

（3）如图2，BC＝4，点D是以BC为直径的半圆上不同于B、C的一个动点，以BD为边作等边△ABD，请求出AC的最值，并说明理由．

Answer 1

【答案】[解决问题]（1）OC＝AE，（2）OC的最大值为3．[迁移拓展]（3）AC的最大值为2+2．AC的最小值为2﹣2．

【解析】

（1）结论：OC=AE．只要证明△CBO≌△ABE即可；
（2）当E、O、A共线，AE有最大值，此时OC有最大值，据此求解即可；
（3）当点A在线段BD的左侧时，以BC为边作等边三角形△BCM，由△ABC≌△DBM，推出AC=MD，推出欲求AC的最大值，只要求出DM的最大值即可，当点D在BC上方，DM⊥BC时，DM的值最大；当点A在线段BD的左侧时，同理可求AC的最小值.

解：【解决问题】

（1）如图1中，结论：OC＝AE，

理由：∵△ABC，△BOE都是等边三角形，

∴BC＝BA，BO＝BE，∠CBA＝∠OBE＝60°，

∴∠CBO＝∠ABE，

∴△CBO≌△ABE（SAS），

∴OC＝AE．

（2）在△AOE中，AE≤OE+OA，

∴当E、O、A共线，

∴AE的最大值为3，

∴OC的最大值为3．

【迁移拓展】

（3）如图2中，以BC为边作等边三角形△BCM，

∵∠ABD＝∠CBM＝60°，

∴∠ABC＝∠DBM，且AB＝DB，BC＝BM，

∴△ABC≌△DBM（SAS），

∴AC＝MD，

∴欲求AC的最大值，只要求出DM的最大值即可，

∵BC＝4＝定值，∠BDC＝90°，

∴点D在以BC为直径的⊙O上运动，

由图象可知，当点D在BC上方，DM⊥BC时，DM的值最大，最大值＝2+2 ，

∴AC的最大值为2+2 ．

当点A在线段BD的右侧时，同理可得AC的最小值为2-2．

综上所述AC的最大值为2+2 ，最小值为2-2.