��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���O�İ뾶Ϊ1��P������ϵ������һ�㣬��P����O�ľ���SP�Ķ������£�����P��Բ��O�غϣ���SPΪ��O�İ뾶��������P��Բ��O���غϣ�������OP����O�ڵ�A����SPΪ�߶�AP�ij��ȣ�
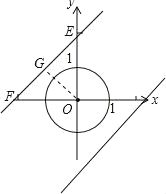
ͼ1Ϊ��P����O�������ʾ��ͼ��
��1������B��1��0����C��1��1����D��0��![]() ������SB= ��SC= ��SD= ��
������SB= ��SC= ��SD= ��
��2����ֱ��y=x+b�ϴ��ڵ�M��ʹ��SM=2����b��ȡֵ��Χ��
��3����֪��P��Q��x���ϣ�RΪ�߶�PQ������һ�㣮���߶�PQ�ϴ���һ��T������T����O����ST��SR��ֱ��д�������������߶�PQ���ȵ����ֵ��
���𰸡���1��0��![]() ��1��
��1��![]() ��
��
��2��b��ȡֵ��Χ����3![]() ��b��3
��b��3![]() ��
��
��3���߶�PQ���ȵ����ֵΪ1+2+1=4��
��������
�����������1�����ݵ��������¶����ɣ�
��2������ֱ��y=x+b���ص㣬���SM=2�����ݵ���ֱ�������ε����ʽ��
��3������T����O�ڣ�ȷ��ST�ķ�Χ�����ݸ��������������ͼ����������������߶�PQ���ȵ����ֵ��
�����������1������B��1��0������SB=0����C��1��1������SC=![]() ��1����D��0��
��1����D��0��![]() ������SD=
������SD=![]() ���ʴ�Ϊ��0��
���ʴ�Ϊ��0��![]() ��1��
��1��![]() ,��
,��
��2����ֱ��y=x+b��ֱ���x�ᡢy�ύ��F��E����OG��EF��G��
�ߡ�FEO=45������OG=GE����OG=3ʱ��GE=3��
�ɹ��ɶ����ã�OE=3![]() ����ʱֱ�ߵĽ���ʽΪ��y=x+3
����ʱֱ�ߵĽ���ʽΪ��y=x+3![]() ��
��
��ֱ��y=x+b�ϴ��ڵ�M��ʹ��SM=2��b��ȡֵ��Χ����3![]() ��b��3
��b��3![]() ��
��
��3����T����O�ڣ���ST��1����ST��SR����SR��1��
���߶�PQ���ȵ����ֵΪ1+2+1=4��