题目内容
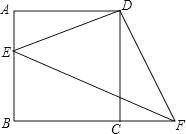
【题目】如图,四边形ABCD是正方形,E点在AB上,F点在BC的延长线上,且CF=AE,连接DE、DF、EF.
①求证:△ADE≌△CDF;
②填空:△CDF可以由△ADE绕旋转中心 点,按逆时针方向旋转 度得到;
③若BC=3,AE=1,求△DEF的面积.
【答案】(1)详见解析;(2)D,90;
【解析】
试题分析:(1)根据SAS即可证得;(2)根据旋转的定义即可解答;(3)根据S△BEF=S梯形ABFD﹣S△ADE﹣S△BEF即可求解.
试题解析:(1)证明:∵正方形ABCD中,∠A=∠BCD=90°,则∠DCF=∠A=90°,AD=CD,
在△ADE和△CDF中,
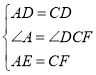 ,
,
∴△ADE≌△CDF;
(2)△CDF可以由△ADE绕旋转中心D点,按逆时针方向旋转90度得到.
(3)AD=AB=BC=3,CF=AE=1,
则S梯形ABFD=![]() (AD+BF)AB=
(AD+BF)AB=![]() ×(3+4)×3=18,
×(3+4)×3=18,
S△ADE=![]() AEAD=
AEAD=![]() ×1×3=
×1×3=![]() ;
;
S△BEF=![]() BEBF=
BEBF=![]() ×2×(3+1)=4,
×2×(3+1)=4,
则S△DEF=18﹣![]() ﹣4=
﹣4=![]() .
.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目