题目内容
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围 ;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
【答案】(1)二次函数解析式为y=x2﹣3x.(2)故答案为﹣![]() ≤y<4.(3)当BC=1时,矩形的周长为6.
≤y<4.(3)当BC=1时,矩形的周长为6.
【解析】
试题分析:(1)把(0,0)代入抛物线解析式求出m的值,再根据增减性确定m的值即可.
(2)画出函数图象,求出函数最小值以及x=0或4是的y的值,由此即可判断.
(3)由BC=1,B、C关于对称轴对称,推出B(,1,0),C((2,0),由AB⊥x轴,DC⊥x轴,推出A(1,﹣2),D(2,﹣2),求出AB,即可解决问题.
试题解析:(1)∵y=x2+(2m﹣1)x+m2﹣1经过坐标原点,
∴0=0+0+m2﹣1,即m2﹣1=0,解得m=±1.
又∵当x<0时,y随x的增大而减小,,∴m=﹣1,
∴二次函数解析式为y=x2﹣3x.
(2)如图1中,

x=0时,y=0,∵y=(x﹣![]() )2﹣
)2﹣![]() ,∴x=
,∴x=![]() 时,y最小值为﹣
时,y最小值为﹣![]() ,
,
x=4时,y=4,∴0<x<4时,﹣![]() ≤y<4.
≤y<4.
故答案为﹣![]() ≤y<4.
≤y<4.
(3)如图2中,
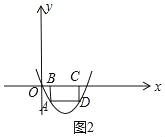
∵BC=1,B、C关于对称轴对称,∴B(,1,0),C((2,0),∵AB⊥x轴,DC⊥x轴,
∴A(1,﹣2),D(2,﹣2),∴AB=DC=2,BC=AD=1,
∴四边形ABCD的周长为6,
当BC=1时,矩形的周长为6.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】在一次体育达标测试中,九年级(3)班的15名男同学的引体向上成绩如下表所示:
成绩(个) | 8 | 9 | 11 | 12 | 13 | 15 |
人数 | 1 | 2 | 3 | 4 | 3 | 2 |
这15名男同学引体向上成绩的中位数和众数分别是( )
A.12,13
B.12,12
C.11,12
D.3,4