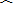题目内容
如图,在⊙O中,∠ACB=∠BDC=60°,AC=2
cm.
(1)求∠BAC的度数;(2)求⊙O的周长.

| 3 |
(1)求∠BAC的度数;(2)求⊙O的周长.

(1)∠BAC=∠BDC=60°(同弧所对的圆周角相等);
(2)∠ABC=180°-∠BAC-∠ACB=60°,
∴△ABC是等边三角形,
作OE⊥AC于点E,连接OA,则OA平分∠BAC,
∴∠OAE=30°,
∴OA=
=
=2cm,
所以⊙O的周长=2π×2=4πcm.
(2)∠ABC=180°-∠BAC-∠ACB=60°,
∴△ABC是等边三角形,
作OE⊥AC于点E,连接OA,则OA平分∠BAC,
∴∠OAE=30°,
∴OA=
| AE |
| cos∠OAE |
| ||
| cos30° |
所以⊙O的周长=2π×2=4πcm.


练习册系列答案
相关题目