题目内容
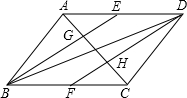 如图,在?ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,试判断下列结论:①△ABE≌△CDF;②AG=HC;③EG=CH;④S△ABE=S△BDF,其中正确的结论是
如图,在?ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,试判断下列结论:①△ABE≌△CDF;②AG=HC;③EG=CH;④S△ABE=S△BDF,其中正确的结论是①②④
①②④
.分析:根据三角形全等的判定,由已知条件可证①△ABE≌△CDF;继而证△AGE≌△CHF,可判断②、③;根据△ABE与△BFD底相等,高相等,即可判断④.
解答:解:在?ABCD中,AB=CD,∠BAE=∠DCF,BC=DA;
∵E、F分别是边AD、BC的中点,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),故①正确;
∵△ABE≌△CDF,
∴∠AEG=∠CFH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(ASA),
∴AG=HC,故②正确;
若EG=CH,则EG=AG,∠GAE=∠GEA,而这根据题意是无法判断的,故③错误;
∵△ABE与△BFD底相等,高相等,
∴S△ABE=S△BDF,故④正确.
综上可得共有3个结论正确.
故答案为:3.
∵E、F分别是边AD、BC的中点,
∴AE=CF,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(SAS),故①正确;
∵△ABE≌△CDF,
∴∠AEG=∠CFH,
在△AGE和△CHF中,
|
∴△AGE≌△CHF(ASA),
∴AG=HC,故②正确;
若EG=CH,则EG=AG,∠GAE=∠GEA,而这根据题意是无法判断的,故③错误;
∵△ABE与△BFD底相等,高相等,
∴S△ABE=S△BDF,故④正确.
综上可得共有3个结论正确.
故答案为:3.
点评:本题考查了平行四边形的性质和平行线等分线段定理与全等三角形的判定,中等难度,解答此类题目的关键是熟记平行四边形的几个重要的性质.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=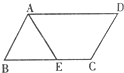 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.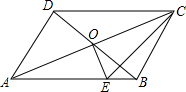 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是