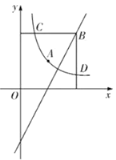
题目内容
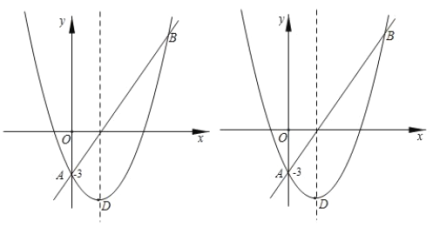
【题目】将一个直角三角形纸片![]() ,放置在平面直角坐标系中,点
,放置在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]()
(I)过边![]() 上的动点
上的动点![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合)作
重合)作![]() 交
交![]() 于点
于点![]() ,沿着
,沿着![]() 折叠该纸片,点
折叠该纸片,点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处.
处.
①如图,当![]() 为
为![]() 中点时,求
中点时,求![]() 点的坐标;
点的坐标;
②连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 点坐标:
点坐标:
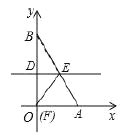
(Ⅱ)![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() 重合),将
重合),将![]() 沿
沿![]() 所在的直线折叠,得到
所在的直线折叠,得到![]() ,连接
,连接![]() ,当
,当![]() 取得最小值时,求
取得最小值时,求![]() 点坐标(直接写出结果即可).
点坐标(直接写出结果即可).

【答案】(I)①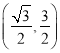 ;②
;②![]() 点坐标为
点坐标为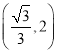 或
或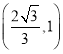 ;(II)
;(II)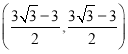
【解析】
(I)①过点E做EH⊥OA ,交OA于点H,由D为OB中点结合DE∥OA,可得出DE为△BOA的中位线,再根据点A、B的坐标即可得出点E的坐标;
②根据折叠的性质结合角的计算可得出∠AEF=60°≠90°,分∠AFE=90°和∠EAF=90°两种情况考虑,利用含30度角的直角三角形以及勾股定理即可求出点E的坐标;
(II)根据三角形的三边关系,找出当点A′在y轴上时,BA′取最小值,根据折叠的性质可得出直线OP的解析式,再根据点A、B的坐标利用待定系数法求出直线AB的解析式,联立两直线解析式成方程组,解之即可得出点P的坐标.
(I)过点E做EH⊥OA ,交OA于点H,

①∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 中点,
中点,
∴D点的坐标为![]() ,
,
∴![]() 为
为![]() 的中位线,
的中位线,
∴点![]() 为线段
为线段![]() 的中点,
的中点,
又∵![]() ,
,
∴EH为![]() 的中位线,
的中位线,
∴点H为线段OA的中点,
∴点H的坐标为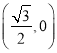 ,
,
∴点![]() 的坐标为
的坐标为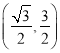 .
.
②∵点![]() ,点
,点![]() ,
,
∴![]() ,OB=3
,OB=3
∴![]() ,
,
∴∠B=30°,
由折叠可知:![]() .
.
∴![]() ,
,![]()
∴![]() .
.
∵![]() 是直角三角形,
是直角三角形,
∴![]() 或
或![]()
(i)当![]() 时,如图1所示
时,如图1所示
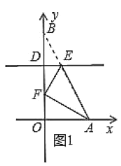
![]() .
.
在![]() 中,
中,![]() ,
,![]()
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∵![]() .
.
∴点![]() 的坐标为
的坐标为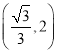 ;
;
(ii)当![]() 时,如图2所示.
时,如图2所示.

∵![]() ,
,![]()
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴点![]() 的坐标为
的坐标为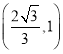 .
.
综上所述:当![]() 为直角三角形时,
为直角三角形时,![]() 点坐标为
点坐标为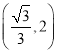 或
或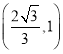 .
.
(II)由折叠可知:![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
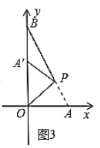
∴当点![]() 在
在![]() 轴上时,
轴上时,![]() 取最小值,如图3所示.
取最小值,如图3所示.
∵![]()
∴![]()
∴直线![]() 的解析式为
的解析式为![]()
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 、
、![]() 代入
代入![]() 中,
中,
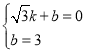 ,解得:
,解得: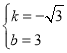 ,
,
∴直线![]() 的解忻式为
的解忻式为![]() .
.
联立直线![]() 、
、![]() 的解析式成方程组,
的解析式成方程组,
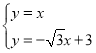 ,解得:
,解得: ,
,
∴.当![]() 取得最小值时,
取得最小值时,![]() 点坐标为
点坐标为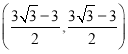 .
.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案