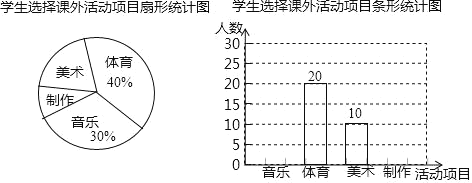
题目内容
【题目】对于下列结论:
①二次函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
②关于![]() 的方程
的方程![]() 的解是
的解是![]() ,
,![]() (
(![]() 、
、![]() 、
、![]() 均为常数,
均为常数,![]() ),则方程
),则方程![]() 的解是
的解是![]() ,
,![]() .
.
③设二次函数![]() ,当
,当![]() 时,总有
时,总有![]() ,当
,当![]() 时,总有
时,总有![]() ,那么
,那么![]() 的取值范围是
的取值范围是![]() .
.
其中,正确结论的个数是( )
A.0个B.1个C.2个D.3个
【答案】C
【解析】
根据二次函数的开口方向和对称轴方程,即可判断①,根据一元二次方程的根的定义,即可判断②,由二次函数![]() ,当
,当![]() 时,总有
时,总有![]() ,可得函数图象过点(1,0),由当
,可得函数图象过点(1,0),由当![]() 时,总有
时,总有![]() ,可得抛物线与x轴的另一个交点横坐标≥3,即可判断③.
,可得抛物线与x轴的另一个交点横坐标≥3,即可判断③.
①![]() 在二次函数
在二次函数![]() 中,
中,![]() ,
,![]() ,
,
![]() 抛物线的对称轴为
抛物线的对称轴为![]() 轴,开口向上,
轴,开口向上,
∴当![]() 时,
时,![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() ①结论正确;
①结论正确;
②![]() 关于
关于![]() 的方程
的方程![]() 的解是
的解是![]() ,
,![]() ,
,
![]() 或
或![]() ,
,
![]() 方程
方程![]() 中,
中,![]() 或
或![]() ,
,
解得:![]() ,
,![]() ,
,
![]() ②结论错误;
②结论错误;
③![]() 二次函数
二次函数![]() ,当
,当![]() 时,总有
时,总有![]() ,当
,当![]() 时,总有
时,总有![]() ,
,
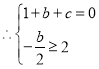 ,
,
解得:![]() ,
,![]() ,
,
∴结论③正确.
故选C.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
【题目】某校九年级( 3 )班全体学生 2019 年初中毕业体育考试的成绩统计如下表:
成绩 | 35 | 39 | 42 | 43 | 45 | 49 | 50 |
人数 | 3 | 5 | 6 | 6 | 8 | 7 | 5 |
根据上表中的信息判断,下列结论中错误的是 ( )
A.该班一共有 40 名同学B.该班学生这次考试成绩的众数是 45 分
C.该班学生这次考试成绩的中位数是 44 分D.该班学生这次考试成绩的平均数是 45 分