题目内容
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值
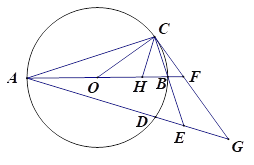
【答案】(1)证明见解析;(2)①证明见解析;②5.
【解析】
(1)由题意可知:∠CAB=∠GAF,由圆的性质可知:∠CAB=∠OCA,所以∠OCA=∠GCE,从而可证明直线CG是⊙O的切线;
(2)①由于CB=CH,所以∠CBH=∠CHB,易证∠CBH=∠OCB,从而可证明△CBH∽△OBC;
②由△CBH∽△OBC可知:![]() ,所以HB=
,所以HB=![]() ,由于BC=HC,所以OH+HC=4
,由于BC=HC,所以OH+HC=4![]() +BC,利用二次函数的性质即可求出OH+HC的最大值.
+BC,利用二次函数的性质即可求出OH+HC的最大值.
(1)由题意可知:∠CAB=∠GAF,
∵AB是⊙O的直径,
∴∠ACB=90°
∵OA=OC,
∴∠CAB=∠OCA,
∴∠OCA+∠OCB=90°,
∵∠GAF=∠GCE,
∴∠GCE+∠OCB=∠OCA+∠OCB=90°,
∵OC是⊙O的半径,
∴直线CG是⊙O的切线;
(2)①∵CB=CH,
∴∠CBH=∠CHB,
∵OB=OC,
∴∠CBH=∠OCB,
∴△CBH∽△OBC
②由△CBH∽△OBC可知:![]()
∵AB=8,
∴BC2=HBOC=4HB,
∴HB=![]() ,
,
∴OH=OB-HB=4-![]()
∵CB=CH,
∴OH+HC=4![]() +BC,
+BC,
当∠BOC=90°,
此时BC=4![]()
∵∠BOC<90°,
∴0<BC<4![]() ,
,
令BC=x则CH=x,BH=![]()
![]()
当x=2时,
∴OH+HC可取得最大值,最大值为5

练习册系列答案
相关题目