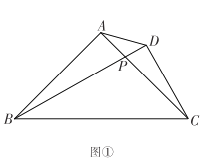
ЬтФПФкШн
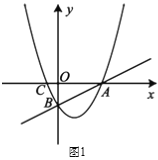
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxoyжаЃЌЕуA (-4,-2)ЃЌНЋЕуAЯђгвЦНвЦ6ИіЕЅЮЛГЄЖШЃЌЕУЕНЕуB.

ЃЈ1ЃЉШєХзЮяЯпyЃН-x2ЃЋbxЃЋcОЙ§ЕуA,BЃЌЧѓДЫЪБХзЮяЯпЕФБэДяЪНЃЛ
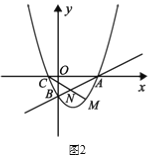
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЕФХзЮяЯпЖЅЕуЮЊCЃЌЕуDЪЧжБЯпBCЩЯвЛЖЏЕуЃЈВЛгыBЃЌCжиКЯЃЉЃЌЪЧЗёДцдкЕуDЃЌЪЙЁїABCКЭвдЕуA,B,DЙЙГЩЕФШ§НЧаЮЯрЫЦЃПШєДцдкЃЌЧыЧѓГіДЫЪБDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
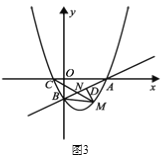
ЃЈ3ЃЉШєХзЮяЯпyЃН-x2ЃЋbxЃЋcЕФЖЅЕудкжБЯпyЃНxЃЋ2ЩЯвЦЖЏЃЌЕБХзЮяЯпгыЯпЖЮ![]() гаЧвжЛгавЛИіЙЋЙВЕуЪБЃЌЧѓХзЮяЯпЖЅЕуКсзјБъtЕФШЁжЕЗЖЮЇЃЎ
гаЧвжЛгавЛИіЙЋЙВЕуЪБЃЌЧѓХзЮяЯпЖЅЕуКсзјБъtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН-x2-2xЃЋ6ЃЛЃЈ2ЃЉДцдкЃЌD (![]() ,
,![]() )ЃЛЃЈ3ЃЉ-4ЁмtЃМ-3Лђ0ЃМtЁм5ЃЎ
)ЃЛЃЈ3ЃЉ-4ЁмtЃМ-3Лђ0ЃМtЁм5ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуAЕФзјБъНсКЯЯпЖЮABЕФГЄЖШЃЌПЩЕУГіЕуBЕФзјБъЃЌИљОнЕуAЃЌBЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉгЩХзЮяЯпНтЮіЪНЃЌЧѓГіЖЅЕуCЕФзјБъЃЌДгЖјЧѓГіжБЯпBCНтЮіЪНЃЌЩшD (d,-3d+4)ЃЌ
ИљОнвбжЊПЩжЊAD=AB=6ЪБЃЌЁїABCЁзЁїBADЃЌДгЖјСаГіЙигкdЕФЗНГЬЃЌНтЗНГЬМДПЩЧѓНтЃЛ
ЃЈ3ЃЉНЋХзЮяЯпЕФБэДяЪНБфаЮЮЊЖЅЕуЪБЃЌвРДЫДњШыЕуAЃЌBЕФзјБъЧѓГіtЕФжЕЃЌдйНсКЯЭМаЮМДПЩЕУГіЃКЕБХзЮяЯпгыЯпЖЮABгаЧвжЛгавЛИіЙЋЙВЕуЪБtЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉЁпЕуAЕФзјБъЮЊЃЈ-4ЃЌ-2ЃЉЃЌНЋЕуAЯђгвЦНвЦ6ИіЕЅЮЛГЄЖШЕУЕНЕуBЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ2ЃЌ-2ЃЉЃЎ
ЁпХзЮяЯпyЃН-x2+bxЃЋcЙ§Еу![]() ЃЌ
ЃЌ
Ёр![]() , НтЕУ
, НтЕУ![]()
ЁрХзЮяЯпБэДяЪНЮЊyЃН-x2-2xЃЋ6
ЃЈ2ЃЉДцдк.
ШчЭМ
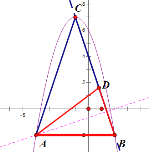
гЩЃЈ1ЃЉЕУЃЌyЃН-x2-2xЃЋ6ЃН-(x+1)2ЃЋ7ЃЌ
ЁрC (-1,7)
ЩшжБЯпBCНтЮіЪНЮЊyЃНkxЃЋb
Ёр![]() НтжЎЕУЃЌ
НтжЎЕУЃЌ![]()
ЁрlBCЃКyЃН-3xЃЋ4
ЩшD (d,-3d+4)ЃЌ
ЁпдкЁїABCжаAC=BC
ЁрЕБЧвНіЕБAD=AB=6ЪБЃЌСНШ§НЧаЮЯрЫЦ
МД(-4-d)2+(-2+3d-4)2=36ЪБЃЌЁїABCЁзЁїBADЃЌ
НтжЎЕУЃЌd1=![]() ЁЂd2=2(ЩсШЅ)
ЁЂd2=2(ЩсШЅ)
ЁрДцдкЕуDЃЌЪЙЁїABCКЭвдЕуA,B,DЙЙГЩЕФШ§НЧаЮЯрЫЦЃЌДЫЪБЕуD (![]() ,
,![]() )ЃЛ
)ЃЛ
ЃЈ3ЃЉШчЭМЃК
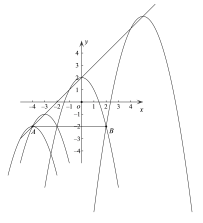
ХзЮяЯпyЃН-x2+bxЃЋcЖЅЕудкжБЯп![]() ЩЯ
ЩЯ
ЁрХзЮяЯпЖЅЕузјБъЮЊ![]()
ЁрХзЮяЯпБэДяЪНПЩЛЏЮЊ![]() ЃЎ
ЃЎ
Аб![]() ДњШыБэДяЪНПЩЕУ
ДњШыБэДяЪНПЩЕУ![]()
НтЕУ![]() ЃЎ
ЃЎ
гжЁпХзЮяЯпгыЯпЖЮABгаЧвжЛгавЛИіЙЋЙВЕуЃЌ
Ёр-4ЁмtЃМ-3ЃЎ
Аб![]() ДњШыБэДяЪНПЩЕУ
ДњШыБэДяЪНПЩЕУ![]() ЃЎ
ЃЎ
НтЕУ![]() ЃЌ
ЃЌ
гжЁпХзЮяЯпгыЯпЖЮABгаЧвжЛгавЛИіЙЋЙВЕуЃЌ
Ёр0ЃМtЁм5ЃЎ
злЩЯПЩжЊ![]() ЕФШЁжЕЗЖЮЇЪБ-4ЁмtЃМ-3Лђ0ЃМtЁм5ЃЎ
ЕФШЁжЕЗЖЮЇЪБ-4ЁмtЃМ-3Лђ0ЃМtЁм5ЃЎ

 ПЮПЮСЗНЫеЯЕСаД№АИ
ПЮПЮСЗНЫеЯЕСаД№АИ УћХЦжабЇПЮЪБзївЕЯЕСаД№АИ
УћХЦжабЇПЮЪБзївЕЯЕСаД№АИ