题目内容
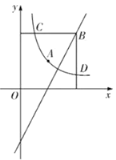
【题目】在平面直角坐标系中,我们定义:横坐标与纵坐标均为整数的点为整点如图,已知双曲线![]() 经过点
经过点![]() ,记双曲线与两坐标轴之间的部分为
,记双曲线与两坐标轴之间的部分为![]() (不含双曲线与坐标轴).
(不含双曲线与坐标轴).
(1)求![]() 的值;
的值;
(2)求![]() 内整点的个数;
内整点的个数;
(3)设点![]() 在直线
在直线![]() 上,过点
上,过点![]() 分别作平行于
分别作平行于![]() 轴
轴![]() 轴的直线,交双曲线
轴的直线,交双曲线![]()
![]() 于点
于点![]() ,记线段
,记线段![]() 、双曲线所围成的区域为
、双曲线所围成的区域为![]() ,若
,若![]() 内部(不包括边界)不超过
内部(不包括边界)不超过![]() 个整点,求
个整点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 内整点的个数为
内整点的个数为![]() 个;(3)若
个;(3)若![]() 内部(不包括边界)不超过
内部(不包括边界)不超过![]() 个整点,
个整点,![]()
【解析】
(1)利用待定系数法即可求解;
(2)将G内x=1,2,3,4分别代入双曲线,即可求出整点;
(3)根据m的情况进行分类讨论,具体见解析.
(1)∵![]() 经过点A(2,2),
经过点A(2,2),
∴![]() ,
,
∴![]() ,
,
(2)对于双曲线![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 在直线
在直线![]() 上,当0
上,当0![]() 时,有整点(1,1)、(1,2)、(1,3),
时,有整点(1,1)、(1,2)、(1,3),
当![]() 时,
时,![]() ,
,
![]() 在直线
在直线![]() 上,当0
上,当0![]() 时,有整点(2,1),
时,有整点(2,1),
当![]() 时,
时,![]() ,
,
![]() 在直线
在直线![]() 上,当0
上,当0![]() 时,有整点(3,1),
时,有整点(3,1),
当![]() 时,
时,![]() ,
,
![]() 在直线
在直线![]() 上,当0
上,当0![]() 时,没有整点.
时,没有整点.
∴G内整点的个数为5个.
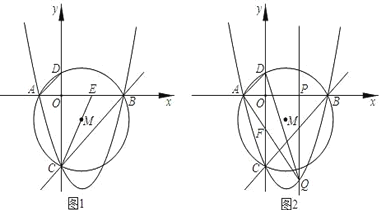
(3)如图,当![]() 时,点B(4,4), 点C(1,4)此时在区域W内(不包含边界)有(2,3)、(3,2)、(3,3)共3个整点,线段BD上有4个整点,线段BC上有4个整点,
时,点B(4,4), 点C(1,4)此时在区域W内(不包含边界)有(2,3)、(3,2)、(3,3)共3个整点,线段BD上有4个整点,线段BC上有4个整点,
∵点(4,4)重合,点(4,1)(1,4)在边界上,
∴当![]() 时,区域W内至少有3+4+4-3=8个整点,
时,区域W内至少有3+4+4-3=8个整点,
当![]() 时,B'(4.5,5),C(
时,B'(4.5,5),C(![]() ),
),
线段B'C'上有4个整点,此时区域W内整点个数为8个,
当![]() 时,区域W内部整点个数增加,
时,区域W内部整点个数增加,
![]() 若W内部(不包括边界)不超过8个整点,
若W内部(不包括边界)不超过8个整点,![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】某校九年级( 3 )班全体学生 2019 年初中毕业体育考试的成绩统计如下表:
成绩 | 35 | 39 | 42 | 43 | 45 | 49 | 50 |
人数 | 3 | 5 | 6 | 6 | 8 | 7 | 5 |
根据上表中的信息判断,下列结论中错误的是 ( )
A.该班一共有 40 名同学B.该班学生这次考试成绩的众数是 45 分
C.该班学生这次考试成绩的中位数是 44 分D.该班学生这次考试成绩的平均数是 45 分