Question

【题目】（问题背景）

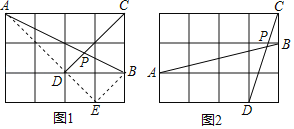
如图1，在边长为1的正方形网格中，连结格点A、B和C、D，AB和CD相交于点P，求tan∠CPB的值．小马同学是这样解决的：连结格点B、E可得BE∥CD，则∠ABE＝∠CPB，连结AE，那么∠CPB就变换到Rt△ABE中．则tan∠CPB的值为　 　．

（探索延伸）

如图2，在边长为1的正方形网格中，AB和CD相交于点P，求sin∠APD的值．

Answer 1

【答案】【问题背景】3；【探索延伸】sin∠APD＝ .

【解析】

（1）在Rt△ABE中，利用正切函数的定义求出tan∠ABE即可．

（2）如图2，连接CE，DE，作DM⊥CE于M．先证明四边形ABCE是平行四边形，得出CE∥AB，那么∠APD＝∠ECD．利用割补法求出△ECD的面积＝，由勾股定理求出CE＝，那么根据三角形的面积公式得出DM＝，然后利用正弦函数定义求出sin∠ECD即可．

解：（1）如图1，

∵BE∥CD，

∴∠ABE＝∠CPB，

∴tan∠ABE＝tan∠CPB，

∵∠AEB＝90°，

∴tan∠CPB＝tan∠ABE＝＝3，

故答案为3．

（2）如图2，连接CE，DE，作DM⊥CE于M．

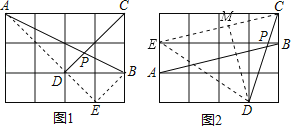
∵BC∥AE，BC＝AE，

∴四边形ABCE是平行四边形，

∴CE∥AB，

∴∠APD＝∠ECD．

∵△ECD的面积＝3×4﹣×1×4﹣×2×3﹣×1×3＝，

∴CEDM＝，

∵CE＝，

∴DM＝，

∴sin∠APD＝sin∠ECD＝．