题目内容
已知两个相似多边形的周长比为1:2,它们的面积和为25,则这两个多边形的面积分别是 和 。
5,20
分析:根据相似多边形周长的比等于相似比,而面积的比等于相似比的平方,即可求得面积的比值,依据面积和为25,就可求得两个多边形的面积.
解:多边形的面积的比是:(1:2)2=1:4,设两个多边形中较小的多边形的面积是x,则较大的面积是4x.
根据题意得:x+4x=25
解得x=5.
因而这两个多边形的面积分别是5和20.
点评:本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方.
解:多边形的面积的比是:(1:2)2=1:4,设两个多边形中较小的多边形的面积是x,则较大的面积是4x.
根据题意得:x+4x=25
解得x=5.
因而这两个多边形的面积分别是5和20.
点评:本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
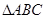 与
与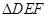 相似且面积的比为
相似且面积的比为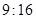 ,则
,则 x+
x+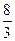 与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.
与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.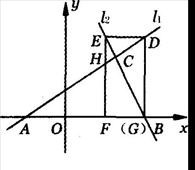
 若AB=4,S ABCD=
若AB=4,S ABCD=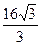 ,求AE的长
,求AE的长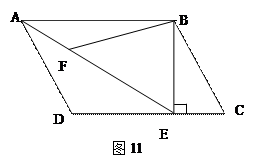
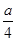 =
=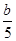 =
= ,且a-b+c=10,则a+b-c的值为( )
,且a-b+c=10,则a+b-c的值为( )
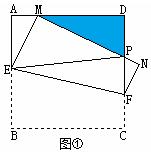
 , EF⊥DE
, EF⊥DE 的长;
的长; 的长.
的长.

