题目内容
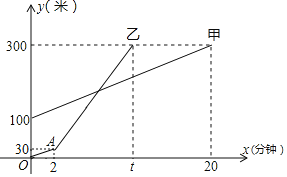
【题目】甲、乙两人相约周末沿同一条路线登山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题
(1)甲登山的速度是每分钟 米;乙在A地提速时,甲距地面的高度为 米;
(2)若乙提速后,乙的速度是甲登山速度的3倍;
①求乙登山全过程中,登山时距地面的高度y(米)与登山时间x(分钟)之间的函数解析式;
②乙计划在他提速后5分钟内追上甲,请判断乙的计划能实现吗?并说明理由;
(3)当x为多少时,甲、乙两人距地面的高度差为80米?
【答案】(1)10,120;(2)①![]() ,②能够实现.理由见解析;(3)当x为2.5或10.5或12时,甲、乙两人距地面的高度差为80米.
,②能够实现.理由见解析;(3)当x为2.5或10.5或12时,甲、乙两人距地面的高度差为80米.
【解析】
(1)由时间,速度,路程的基本关系式可解;
(2)①分段代入相关点的坐标,利用待定系数法来求解即可;
②分别计算甲乙距离地面的高度再比较即可;
(3)求出甲的函数解析式,分0≤x≤2时,2<x≤11时,11<x≤20时来讨论即可求解.
(1)甲登山的速度为:(300﹣100)÷20=10米/分,100+10×2=120米,
故答案为:10,120.
(2)①V乙=3V甲=30米/分,
t=2+(300﹣30)÷30=11(分钟),
设2到11分钟,乙的函数解析式为y=kx+b,
∵直线经过A(2,30),(11,300),
∴![]() 解得
解得![]()
∴当2<x≤11时,y=30x﹣30
设当0≤x≤2时,乙的函数关系式为y=ax,
∵直线经过A(2,30)
∴30=2a解得a=15,
∴当0≤x≤2时,y=15x,
综上,![]()
②能够实现.理由如下:
提速5分钟后,乙距地面高度为30×7﹣30=180米.
此时,甲距地面高度为7×10+100=170米.180米>170米,所以此时,乙已经超过甲.
(3)设甲的函数解析式为:y=mx+100,将(20,300)代入得:300=20m+100
∴m=10,
∴y=10x+100.
∴当0≤x≤2时,由(10x+100)﹣15x=80,解得x=4>2矛盾,故此时没有符合题意的解;
当2<x≤11时,由|(10x+100)﹣(30x﹣30)|=80得
|130﹣20x|=80
∴x=2.5或x=10.5;
当11<x≤20时,由300﹣(10x+100)=80得x=12
∴x=2.5或10.5或12.
∴当x为2.5或10.5或12时,甲、乙两人距地面的高度差为80米.

【题目】我国每年的总用水主要包括四大方面:农业用水、工业用水、生活用水、其他用水. 2017年,我国农业用水量约![]() 亿
亿![]() (占总用水量的
(占总用水量的![]() ),工业用水量约为
),工业用水量约为![]() 亿
亿![]() ,生活用水量具体见下表.
,生活用水量具体见下表.
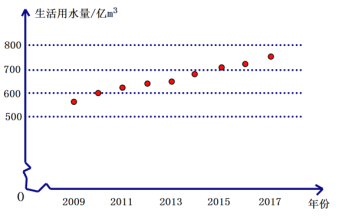
2019-2017年全国生活用水量表(单位:亿![]() )
)
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
用水量 |
|
|
|
|
|
|
|
|
|
(1)2017年全国总用水量约为 亿![]() ,其他用水约为 亿
,其他用水约为 亿![]() .
.
(2)根据“2019-2017年全国生活用水量表”,在平面直角坐标系中描出表中各对数值所对应的点(其中横坐标表示年份,纵坐标表示用水量)可发现,这些点近似的落在某条直线上.
①用靠近尽可能多点的直线来表示用水量的这种趋势,请在上图中画出这条直线;
②根据所画的直线,估计2018年全国生活用水量,并说明理由.
【题目】现在电器进入销售旺季,福清某电器超市销售每台进价分别为![]() 元、
元、![]() 元的
元的![]() 两种型号的电器,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)
两种型号的电器,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
(1)求![]() 两种型号的电器销售单价;
两种型号的电器销售单价;
(2)若超市准备用不超过![]() 元的金额再采购这种型号的电器共
元的金额再采购这种型号的电器共![]() 台,销售完这
台,销售完这![]() 台电器实现利润超过
台电器实现利润超过![]() 元的目标,请给出相应的采购方案;并求出利润的最大值.
元的目标,请给出相应的采购方案;并求出利润的最大值.