题目内容
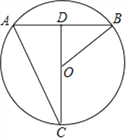
【题目】如图,点C在⊙O上,连接CO并延长交弦AB于点D,![]() ,连接AC、OB,若CD=40,AC=
,连接AC、OB,若CD=40,AC=![]() .
.
(1)求弦AB的长;
(2)求sin∠ABO的值.
【答案】(1)0(2)![]()
【解析】分析:
(1)由CD过圆心O,![]() 可得CD⊥AB,AB=2AD=2BD,结合CD=40,AC=
可得CD⊥AB,AB=2AD=2BD,结合CD=40,AC=![]() 由勾股定理可得AD=20,由此可得AB=2AD=40;
由勾股定理可得AD=20,由此可得AB=2AD=40;
(2)设⊙O的半径为r,在Rt△BDO中由勾股定理建立关于r的方程,解方程求得r的值,即可在Rt△BDO中,由sin∠ABO=![]() 求得sin∠ABO的值.
求得sin∠ABO的值.
详解:
(1)∵CD过圆心O,![]() ,
,
∴CD⊥AB,AB=2AD=2BD,
∴∠ADC=90°,
又∵CD=40,AC=![]() ,
,
∴AD=![]() ,
,
∴AB=2AD=40;
(2)设圆O的半径为r,则OD=CD-OC=40-r,、
∵BD=AD=20,∠ODB=90°,
∴BD2+OD2=OB2,
∴![]() ,
,
解得:![]() ,
,
∴DO=40-25=15,
∴sin∠ABO=![]() .
.

练习册系列答案
相关题目