题目内容
【题目】为落实省新课改精神,某市各校都开设了“知识拓展类”“体艺特长类”“实践活动类”三类拓展性课程.某校为了解在周二第六节开设的“体艺特长类”中各门课程学生的参与情况,随机调查了部分学生作为样本进行统计,绘制了如图所示的统计图(部分信息未给出).
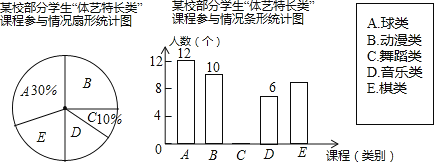
根据图中信息,解答下列问题:
(1)求被调查学生的总人数;
(2)请把条形统计图补充完整;
(3)若该校有150名学生参加了“体艺特长类”中的各门课程,请估计参加棋类的学生人数;
(4)根据调查结果,请你给学校提出一条合理化建议.
【答案】(1)40人;(2)见解析;(3)30人;(4)因为参加A球类的学生人数最多,所以建议学校增加球类课时量,希望学校多点开展拓展性课程,丰富学生的课外生活等等
【解析】
(1)根据“被调查学生的总人数=参加球类的人数÷其所占比例”即可得出结论;
(2)根据“参加舞蹈类的学生人数=被调查学生的总人数×其所占比例”可求出参加舞蹈类的学生人数,继而求得参加棋类的学生人数即可把条形统计图补充完整;
(3)用总人数乘以E棋类所占总体的比例即可得出结论;
(4)根据条形统计图的特点,找出一条建议即可.
(1)12÷30%=40,
答:被调查学生的总人数为40人;
(2)40×10%=4(人),40﹣12﹣10﹣4﹣6=8(人),
补全图形如图所示:
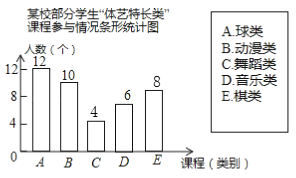
(3)150×![]() =30(人),
=30(人),
答:估计参加棋类的学生人数为30人,
(4)因为参加A球类的学生人数最多,所以建议学校增加球类课时量,希望学校多点开展拓展性课程,丰富学生的课外生活等等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目