Question

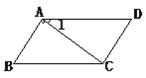
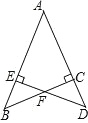
【题目】如图，△ABC，△ADE 均是等腰直角三角形，BC 与 DE 相交于 F 点，若 AC=AE=1，则四边形 AEFC 的周长为________．

Answer 1

【答案】2

【解析】

根据等腰直角三角形的性质和等腰三角形的判定得到 BE=EF=CF=CD，由此得到四边形 AEFC 的周长=AB+AC，根据勾股定理求得AB、AD的长，即可求得四边形 AEFC 的周长．

∵△ABC，△ADE 均是等腰直角三角形，

∴∠B=∠D=45°，∠BEF=∠DCF=90°，

∴△BEF，△DCF 均是等腰直角三角形，

∴BE=EF=CF=CD，

∴四边形 AEFC 的周长=AE+EF+AC+CD=AB+AC，

∵AC=AE=1，

∴AB=AD=，

∴四边形 AEFC 的周长=AE+EF+AC+CD=AB+AC=2.

故答案为：2．