Question

【题目】如图，在长方形 ABCD 中，AB=8，AD=10，点 E 为 BC 上一点，将△ABE 沿 AE 折叠，使点 B 落在长方形内点 F 处， 且 DF=6，求 BE 的长．

Answer 1

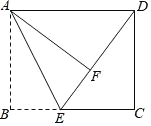
【答案】BE=4．

【解析】

由折叠的性质可知 BE=EF，设 BE=EF=x，然后再依据勾股定理的逆定理可证明△ADF 为直角三角形，则 E、D、F 在一条直线上，在 Rt△CED 中，依据勾股定理列方程求解即可．

解：∵将△ABE 沿 AE 折叠，使点 B 落在长方形内点 F 处，

∴∠AFE=∠B=90°，AB=AF=8，BE=FE．

在△ ADF 中，AF2+DF2=62+82=100=102=AD2，

∴△ADF 是直角三角形，∠AFD=90°．

∴D，F，E 在一条直线上．

设 BE=x，则 EF=x，DE=6+x，EC=10﹣x， 在 Rt△DCE 中，∠C=90°，

∴CE2+CD2=DE2，

即 （10﹣x）2+82=（6+x）2．

∴x=4．

∴BE=4．