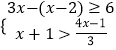题目内容
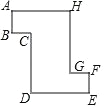
【题目】如图,一块形如“Z”字形的铁皮,每个角都是直角,且 AB=BC=EF=GF=1, CD=DE=GH=AH=3,现将铁片裁剪并拼接成一个和它等面积的正方形,则正方形的边长是_____.
【答案】![]()
【解析】
延长 BC 交 HG 于点 M,延长 HG 交 DE 于点 N,根据“Z”字形的铁皮的面积=S 矩形ABMH+S矩形CDNM+S正方形GFEN计算出不规则铁皮的面积,即可得面积相等的正方形的面积,由此求得正方形的边长即可.
如图所示,延长 BC 交 HG 于点 M,延长 HG 交 DE 于点 N,

则四边形ABMH、CDNM 为矩形,四边形 GFEN 为正方形.
∴“Z”字形的铁皮的面积=S 矩形ABMH+S矩形CDNM+S正方形GFEN
=AHAB+CDDN+GFEF
=3×1+3×2+1×1
=10.
∴正方形的边长=![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目