题目内容
【题目】在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长x与等边△ABC的周长y的关系.

(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是 ; 此时![]() = ;
= ;
(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想( I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.
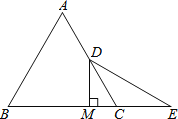
(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.
【答案】(1)BM+NC=MN;![]() ;(2)成立:BM+NC=MN;(3)BM+MN=NC.证明见解析.
;(2)成立:BM+NC=MN;(3)BM+MN=NC.证明见解析.
【解析】
(1)由DM=DN,∠MDN=60°,可证得△MDN是等边三角形,又由△ABC是等边三角形,CD=BD,易证得Rt△BDM≌Rt△CDN,然后由直角三角形的性质,即可求得BM、NC、MN之间的数量关系 BM+NC=MN,此时![]() ;
;
(2)在CN的延长线上截取CM1=BM,连接DM1.可证△DBM≌△DCM1,即可得DM=DM1,易证得∠CDN=∠MDN=60°,则可证得△MDN≌△M1DN,然后由全等三角形的性质,即可得结论仍然成立;
(3)首先在CN上截取CM1=BM,连接DM1,可证△DBM≌△DCM1,即可得DM=DM1,然后证得∠CDN=∠MDN=60°,易证得△MDN≌△M1DN,则可得NC-BM=MN.
解:(1)如图1,BM、NC、MN之间的数量关系BM+NC=MN.
此时![]() .
.
理由:∵DM=DN,∠MDN=60°,
∴△MDN是等边三角形,
∵△ABC是等边三角形,
∴∠A=60°,
∵BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠MBD=∠NCD=90°,
∵DM=DN,BD=CD,
∴Rt△BDM≌Rt△CDN,
∴∠BDM=∠CDN=30°,BM=CN,
∴DM=2BM,DN=2CN,
∴MN=2BM=2CN=BM+CN;
∴AM=AN,
∴△AMN是等边三角形,
∵AB=AM+BM,
∴AM:AB=2:3,
∴![]() ;
;
(2)猜想:结论仍然成立.
证明:在NC的延长线上截取CM1=BM,连接DM1.
∵∠MBD=∠M1CD=90°,BD=CD,
∴△DBM≌△DCM1,
∴DM=DM1,∠MBD=∠M1CD,M1C=BM,
∵∠MDN=60°,∠BDC=120°,
∴∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N=M1C+NC=BM+NC,
∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,
∴![]() ;
;

(3)证明:在CN上截取CM1=BM,连接DM1.
可证△DBM≌△DCM1,
∴DM=DM1,
可证∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N,
∴NC-BM=MN.

 名校课堂系列答案
名校课堂系列答案【题目】在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每一道题,答对得x分,答错或不答扣y分,下表记录了其中两个参赛者的得分情况:
参赛者 | 答对题数 | 答错或不答题数 | 得分 |
A | 18 | 2 | 104 |
B | 13 | 7 | 64 |
(1)求出x和y的值;
(2)若参赛者C的得分要超过80分,则他至少要答对多少道题?