��Ŀ����
����Ŀ���Ķ�������ϣ�
����ѧ���ϣ���ʦ����������⣺��AOB
�߹���ͼ����һ���ǵ�����֪��
��֪����AOB
������һ���ǣ�ʹ�����ڡ�AOB
Сǿ���������£�
�� ������O��A'
�� ��OΪԲ�ģ����ⳤΪ�뾶��������OA��C,��OB��D
�� ��O��ΪԲ�ģ�OCΪ�뾶����C��E��, ����O��A����C��
�� ��C��ΪԲ�ģ�CDΪ�뾶����, ����C��E����D��
�ݹ���D��������O��B��
���ԡ�A��O��B���������Ľ�
��ʦ˵����Сǿ��������ȷ����
��ش�Сǿ��ֱ�ߺ�Բ����ͼ��A��O��B��=��AOB������������ȫ�ȵ��ж������е� ��
�ó���D��O��C��ա�DOC������֤����A��O��B��=��AOB��
���𰸡�SSS
���������⣺������ͼ�ɵ�DO=D��O�䣬CO=C��O�䣬CD=C��D�䣬
���ڡ�COD�͡�C��O��D���� 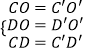 ��
��
���D��O��C��ա�DOC��SSS����
���Դ��ǣ�SSS��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ





