题目内容
【题目】在锐角三角形ABC中,高AD和BE交于点H,且BH=AC,则∠ABC的度数是( )
A.30°
B.45°
C.60°
D.30°或45°
【答案】B
【解析】解: 
∵△ABC为锐角三角形,
∴高AD和BE在三角形内,
∵高AD和BE交于点H,
∴∠ADC=∠BEC=90°.
∵∠EBD+∠BHD=90°,∠AHE+∠HAE=90°,∠BHD=∠AHE,
∴∠EAD=∠EBD,
又∵BH=AC,∠ADC=∠BDH=90°,
在△BDH与△ADC中,
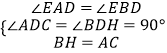 ,
,
∴△BDH≌△ADC(AAS),
∴BD=AD,
∵∠ADB=90°,
∴∠ABC=45°.
故答案为:B.
根据等角的余角相等得出∠EAD=∠EBD,然后利用SAS判断出△BDH≌△ADC根据全等三角形的性质得出BD=AD,由等腰直角三角形的性质得出∠ABC=45°.

练习册系列答案
相关题目


