题目内容
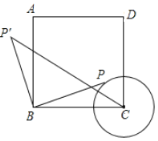
【题目】如图,正方形![]() 中,
中,![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径画
长为半径画![]() ,点
,点![]() 在
在![]() 上移动,连接
上移动,连接![]() ,并将
,并将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() .在点
.在点![]() 移动的过程中,
移动的过程中,![]() 长度的最小值是( )
长度的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
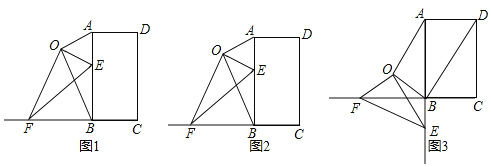
通过画图发现,点![]() 的运动路线为以A为圆心、 1为半径的圆,当
的运动路线为以A为圆心、 1为半径的圆,当![]() 在对角线CA上时,C
在对角线CA上时,C![]() 最小,先证明△PBC≌△
最小,先证明△PBC≌△![]() BA,则
BA,则![]() A=PC=1,再利用勾股定理求对角线CA的长,则得出C
A=PC=1,再利用勾股定理求对角线CA的长,则得出C![]() 的长.
的长.
如图,当![]() 在对角线CA上时,C
在对角线CA上时,C![]() 最小,
最小,
连接CP,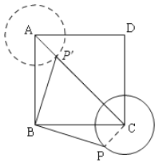
由旋转得:BP=B![]() ,∠PB
,∠PB![]() =90°,
=90°,
∴∠PBC+∠CB![]() =90°,
=90°,
∵四边形ABCD为正方形,
∴BC=BA,∠ABC=90°,
∴∠AB![]() +∠CB
+∠CB![]() =90°,
=90°,
∴∠PBC=∠AB![]() ,
,
在△PBC和△![]() BA中,
BA中,
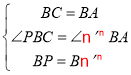 ,
,
∴△PBC≌△![]() BA,
BA,
∴![]() A=PC=1,
A=PC=1,
在Rt△ABC中,AB=BC=4,
由勾股定理得:![]() ,
,
∴C![]() =AC-
=AC-![]() A=
A=![]() ,
,
即C![]() 长度的最小值为
长度的最小值为![]() ,
,
故选:D.

【题目】某校拟派一名跳高运动员参加校际比赛,对甲、乙两名同学进行了8次跳高选拔比赛,他们的原始成绩(单位:cm)如下表:
学生/成绩/次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 |
甲 | 169 | 165 | 168 | 169 | 172 | 173 | 169 | 167 |
乙 | 161 | 174 | 172 | 162 | 163 | 172 | 172 | 176 |
两名同学的8次跳高成绩数据分析如下表:
学生/成绩/名称 | 平均数(单位:cm) | 中位数(单位:cm) | 众数(单位:cm) | 方差(单位:cm2) |
甲 | a | b | c | 5.75 |
乙 | 169 | 172 | 172 | 31.25 |
根据图表信息回答下列问题:
(1)a= ,b= ,c= ;
(2)这两名同学中, 的成绩更为稳定;(填甲或乙)
(3)若预测跳高165就可能获得冠军,该校为了获取跳高比赛冠军,你认为应该选择 同学参赛,理由是: ;
(4)若预测跳高170方可夺得冠军,该校为了获取跳高比赛冠军,你认为应该选择 同学参赛,班由是: .