题目内容
【题目】矩形![]() 中,线段
中,线段![]() 绕矩形外一点
绕矩形外一点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() ,使
,使![]() 点的对应点
点的对应点![]() 落在射线
落在射线![]() 上,
上,![]() 点的对应点
点的对应点![]() 在
在![]() 的延长线上.
的延长线上.
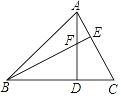
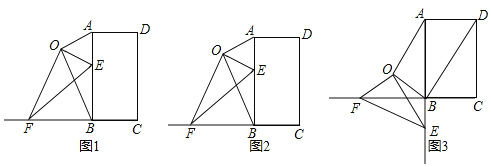
(1)如图1,连接![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 与
与![]() 的大小关系为______________.
的大小关系为______________.
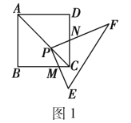
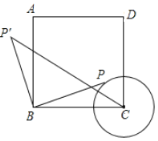
(2)如图2,当点![]() 位于线段
位于线段![]() 上时,求证:
上时,求证:![]() ;
;
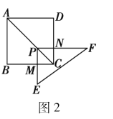
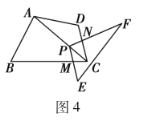
(3)如图3,当点![]() 位于线段
位于线段![]() 的延长线上时,
的延长线上时,![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)相等;(2)见解析;(3)![]()
【解析】
(1)由旋转得:旋转角相等,可得结论;
(2)证明△AOB≌△EOF(SAS),得∠OAB=∠OEF,根据平角的定义可得结论;
(3)如解图,根据等腰三角形的性质得:∠OFB=∠OBF=30°,∠OAE=∠AEO=30°,根据30度角的直角三角形的性质分别求得OB、OG、BF,勾股定理求得BE的长,再根据三角形面积公式即可求得结论.
(1)由旋转得:∠AOE=∠BOF=![]() ,
,
故答案为:相等;
(2)∵![]() ,
,
∴![]() ,
,
在△AOB和△EOF中
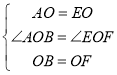 ,
,
∴△AOB≌△EOF(SAS),
∴![]() ,
,
∵OA=OE,
∴![]() ,
,
∴![]()
![]()
![]() ;
;
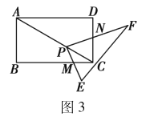
(3)如图,过点O作 ![]() ,垂足为G,
,垂足为G,
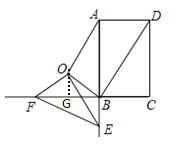
根据旋转的性质知:∠BOF=120°,∠AOB=∠EOF,OB=OF,
△BOF中,∠OFB=∠OBF=30°,
∴∠ABO=60°,
△AOE中,∠AOE=120°,OA=OE,
∴∠OAE=∠AEO=30°,
∴∠AOB=90°,
在△AOB和△EOF中
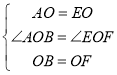 ,
,
∴△AOB≌△EOF(SAS),
∴![]() ,
,
在![]() 中,∠AOB=90°,
中,∠AOB=90°,![]() ,∠OAB=30°,
,∠OAB=30°,
∴![]() ,
,
在![]() 中,∠OGB=90°,
中,∠OGB=90°,![]() ,∠OBG=30°,
,∠OBG=30°,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,∠EBF=90°,
中,∠EBF=90°,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】外线投篮是篮球队常规训练的重要项目之一,下列图表中数据是甲、乙、丙三人每人十次投篮测试的成绩.测试规则为连续投篮十个球为一次,投进篮筐一个球记为1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
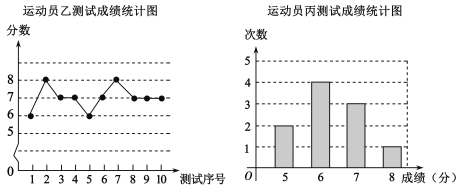
(1)写出运动员乙测试成绩的众数和中位数;
(2)在他们三人中选择一位投篮成绩优秀且较为稳定的选手作为中锋,你认为选谁更合适?为什么?