题目内容
【题目】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
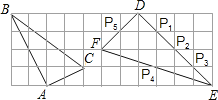
(1)试证明三角形△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似(要求:不写作法与证明).
【答案】(1)证明见解析;(2)相似,(3)作图见解析.
【解析】
试题(1)利用网格得出AB2=20,AC2=5,BC2=25,再利用勾股定理逆定理得出答案即可;
(2)利用AB=2![]() ,AC=
,AC=![]() ,BC=5以及DE=4
,BC=5以及DE=4![]() ,DF=2
,DF=2![]() ,EF=2
,EF=2![]() ,利用三角形三边比值关系得出即可;
,利用三角形三边比值关系得出即可;
(3)根据△P2P4P5三边与△ABC三边长度得出答案即可.
解:(1)∵AB2=20,AC2=5,BC2=25;
∴AB2+AC2=BC2,
根据勾股定理的逆定理得△ABC 为直角三角形;
(2)△ABC和△DEF相似.
由(1)中数据得AB=2![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
DE=4![]() ,DF=2
,DF=2![]() ,EF=2
,EF=2![]() .
.
![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
∴△ABC∽△DEF.
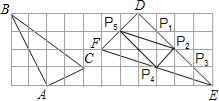
(3)如图:连接P2P5,P2P4,P4P5,
∵P2P5=![]() ,P2P4=
,P2P4=![]() ,P4P5=2
,P4P5=2![]() ,
,
AB=2![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴△ABC∽△P2P4P5.

 特高级教师点拨系列答案
特高级教师点拨系列答案【题目】据《北京晚报》介绍,自2009年故宫博物院年度接待观众首次突破1000万人次之后,每年接待量持续增长,到2018年突破1700万人次,成为世界上接待量最多的博物馆.特别是随着《我在故宫修文物》、《上新了,故宫》等一批电视文博节目的播出,社会上再次掀起故宫热.于是故宫文创营销人员为开发针对不同年龄群体的文创产品,随机调查了部分参观故宫的观众的年龄,整理并绘制了如下统计图表.
2018年参观故宫观众年龄频数分布表
年龄x/岁 | 频数/人数 | 频率 |
20≤x<30 | 80 | b |
30≤x<40 | a | 0.240 |
40≤x<50 | 35 | 0.175 |
50≤x<60 | 37 | c |
合计 | 200 | 1.000 |
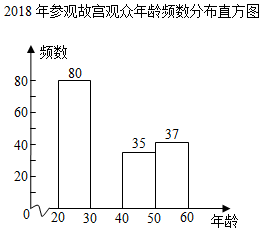
(1)求表中a,b,c的值;
(2)补全频数分布直方图;
(3)从数据上看,年轻观众(20≤x<40)已经成为参观故宫的主要群体.如果今年参观故宫人数达到2000万人次,那么其中年轻观众预计约有 万人次.