题目内容
【题目】在平面直角坐标系中，M（m，n）且m、n满足m2+2n2﹣2mn+4n+4＝0，B（0，b）为y轴上一动点，绕B点将直线BM顺时针旋转45°交x轴于点C，过C作AC⊥BC交直线BM于点A（a，t）．
（1）求点M的坐标；
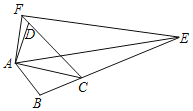
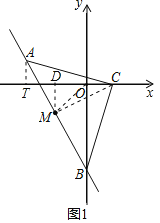
（2）如图1，在B点运动的过程中，A点的横坐标是否会发生变化？若不变，求a的值；若变化，写出A点的横坐标a的取值范围；
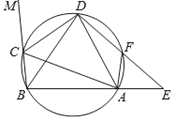
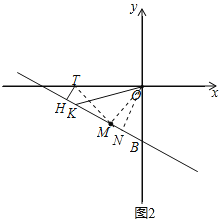
（3）如图2，过T（a，0）作TH⊥BM（垂足H在x轴下方），在射线HB上截取HK＝HT，连OK，求∠OKB的度数．
【答案】(1) 点M的坐标为（﹣2，﹣2）；(2)不变,a=-4；(3) 45°
【解析】
（1）根据非负数的性质分别求出m、n，得到点M的坐标；
（2）过A作AT⊥x轴，MD⊥x轴于D，连接OM，CM，证明△CBO≌△ACT，根据全等三角形的性质得到CT=BO=-b，AT=CO=t，根据等腰直角三角形的性质得到∴M为AB中点，根据中点的性质计算，得到答案；
（3）连TM、OM，过O作ON⊥BM于N，证明△HTM≌△NMO，根据全等三角形的性质，等腰直角三角形的性质解答即可．
（1）m2+2n2﹣2mn+4n+4＝0，
m2+n2﹣2mn+n2+4n+4＝0，
（m﹣n）2+（n+2）2＝0，
则m﹣n＝0，n+2＝0，
解得，m＝﹣2，n＝﹣2，
∴点M的坐标为（﹣2，﹣2）；
（2）过A作AT⊥x轴，MD⊥x轴于D，连接OM，CM，
在Rt△ACB中，∠ABC＝45°，
∴CA＝CB，
∵∠ACB＝90°，
∴∠ACT+∠TCB＝90°，
∵∠BOC＝90°，
∴∠BCO+∠TCB＝90°，
∴∠ACT＝∠CBO，
在△CBO和△ACT中，
，
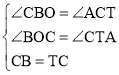∴△CBO≌△ACT（AAS），
∴CT＝BO＝﹣b，AT＝CO＝t，
∴a＝b+t，
∵DO＝DM，
∴∠DOM＝45°，
∴∠MOC＝135°，
∴∠MOC+∠ABC＝180°，
∴O、M、B、C四点共圆，
∴∠CMB＝∠COB＝90°，
∵CA＝CB，
∴M为AB中点，
∴b+t＝﹣4，
∴a＝﹣4；
（3）连TM、OM，过O作ON⊥BM于N，
由（2）可知T（﹣4，0），
∴OT＝4，又点M的坐标为（﹣2，﹣2），
∴△TMO为等腰直角三角形，
∴MT＝MO，
∵∠THM＝90°，∠TMO＝90°，
∴∠TMH＝∠MON，
在△HTM和△NMO中，
，
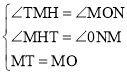∴△HTM≌△NMO（AAS），
∴HT＝MN，HM＝ON，
∴HK＝KN，
∴KN＝ON，
∴∠OKB＝45°．
