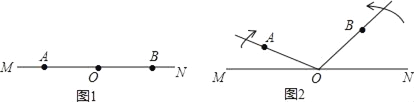题目内容
【题目】数学课上,李老师出示了如下框中的题目.
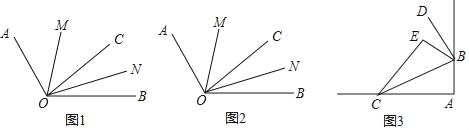
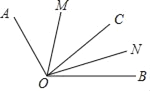
如图1,在∠AOB的内部有一条射线OC把∠AOB分成两个角,射线OM、ON分别平分∠AOC、∠BOC,试探究∠MON与∠AOB之间的数量关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论:
①请你在下表中填上当∠AOB为60°、90°、120°时∠MON的大小:
∠AOB的度数 | 60° | 90° | 120° |
∠MON的度数 |
|
|
|
②探索发现:无论∠AOB的度数是多少,∠MON与∠AOB的数量关系是不变的,请你直接写出结论:
∠MON ∠AOB.
(2)特例启发,解答题目:
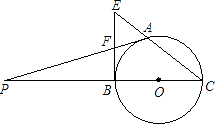
如图2,如果∠AOB=α,请你求∠MON的大小(用α表示).
(3)拓展结论,设计新题:
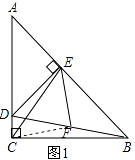
如图3,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,求∠CBD的度数.
【答案】(1)①30°,45°,60°;②![]() ;(2)∠MON=
;(2)∠MON=![]() α;(3)∠CBE+∠EBD=90°.
α;(3)∠CBE+∠EBD=90°.
【解析】
(1)①②根据角平分线的定义即可得到结论;
(2)由角平分线的定义即可得到结论;
(3)先根据折叠的性质得到∠CBA=∠CBE=![]() ∠ABE,再根据平分线的定义得到∠EBD=∠DBM=
∠ABE,再根据平分线的定义得到∠EBD=∠DBM=![]() ∠MBE,则∠CBE+∠EBD=
∠MBE,则∠CBE+∠EBD=![]() (∠ABE+∠MBE)=
(∠ABE+∠MBE)=![]() ∠ABM,然后根据平角定义进行计算.
∠ABM,然后根据平角定义进行计算.
(1)①∵∠MOC=![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠BOC,
∠BOC,
∴∠MON=∠MOC+∠NOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() ∠AOB,
∠AOB,
当∠AOB=60°时,∠MON=![]() ×60°=30°,
×60°=30°,
当∠AOB=90°时,∠MON=![]() ×90°=45°,
×90°=45°,
当∠AOB=120°时,∠MON=![]() ×120°=60°;
×120°=60°;
②由①知,∠MON=![]() ∠AOB,
∠AOB,
(2)由(1)②知,∠MON=![]() ∠AOB,
∠AOB,
∴∠MON=![]() α;
α;
(3)∵A点落在E点处,BC为折痕,
∴∠CBA=∠CBE=![]() ∠ABE,
∠ABE,
∵D是∠EBM的平分线,
∴∠EBD=∠DBM=![]() ∠MBE,
∠MBE,
∴∠CBE+∠EBD=![]() (∠ABE+∠MBE)=
(∠ABE+∠MBE)=![]() ∠ABM=
∠ABM=![]() ×180°=90°.
×180°=90°.