题目内容
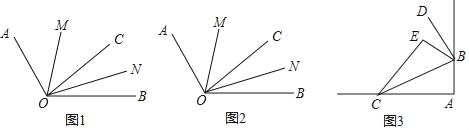
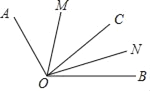
【题目】点A,O,B依次在直线MN上,如图1,现将射线OA绕点O顺时针方向以每秒10°的速度旋转,同时射线OB绕着点O按逆时针方向以每秒15°的速度旋转,直线MN保持不动,如图2,设旋转时间为t秒(t≤12).
(1)在旋转过程中,当t=2时,求∠AOB的度数.
(2)在旋转过程中,当∠AOB=105°时,求t的值.
(3)在旋转过程中,当OA或OB是某一个角(小于180°)的角平分线时,求t的值.
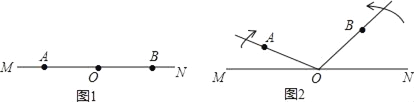
【答案】(1) 130°;(2)t=3或11.4;(3)t=4.5或![]() 或9或
或9或![]()
【解析】
(1)分别求出∠AOM和∠BON的度数,即可得出答案;
(2)分为两种情况,得出方程10t+15t=180-105或10t+15t=180+105,求出方程的解即可;
(3)分为四种情况,列出方程,求出方程的解即可.
(1)当t=2时,∠AOM=10°t=20°,∠BON=15°t=30°,
所以∠AOB=180°﹣∠AOM﹣∠BON=130°;
(2)当∠AOB=105°时,有两种情况:
①10t+15t=180﹣105,解得:t=3;
②10t+15t=180+105,解得:t=11.4;
(3)①当OB是∠AON的角平分线时,10t+15t+15t=180,解得:t=4.5;
②当OA是∠BOM的角平分线时,10t+10t+15t=180,解得:t=![]() ;
;
③当OB是∠AOM的角平分线时,5t+20t=180,解得:t=9;
④当OA是∠BON的角平分线时,10t+7.5t=180,解得:t=![]() .
.

【题目】数学课上,李老师出示了如下框中的题目.
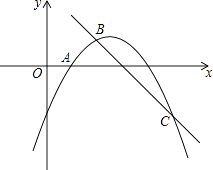
如图1,在∠AOB的内部有一条射线OC把∠AOB分成两个角,射线OM、ON分别平分∠AOC、∠BOC,试探究∠MON与∠AOB之间的数量关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论:
①请你在下表中填上当∠AOB为60°、90°、120°时∠MON的大小:
∠AOB的度数 | 60° | 90° | 120° |
∠MON的度数 |
|
|
|
②探索发现:无论∠AOB的度数是多少,∠MON与∠AOB的数量关系是不变的,请你直接写出结论:
∠MON ∠AOB.
(2)特例启发,解答题目:
如图2,如果∠AOB=α,请你求∠MON的大小(用α表示).
(3)拓展结论,设计新题:
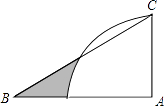
如图3,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,求∠CBD的度数.