题目内容
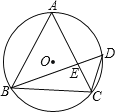
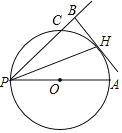
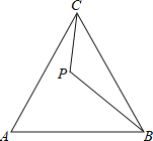
【题目】如图所示,点P位于等边△ABC的内部,且∠ACP=∠CBP.
(1)延长BP至点D,使得PD=PC,连接AD,CD.
①依题意,补全图形;
②证明:AD+CD=BD;
(2)在(1)的条件下,若BD的长为2,求四边形ABCD的面积.
【答案】(1)①见解析;②见解析;(2)![]()
【解析】
(1)①利用延长线作法得出D点位置,并连接AD,CD.
②先证明△CDP是等边三角形,再证明∠DCA≌△PCB,然后利用全等三角形的性质解答即可;
(2)作CM⊥BD于M,AN⊥BD于N,由锐角三角函数的知识得CM=CDsin60°,AN=ADsin60°,然后根据S四边形ABCD=S△BDC+S△BDA计算即可.
解:(1)①如图所示,
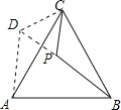
②证明::∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠PCA+∠PCB=60°,
∵∠PCA=∠CBP,
∴∠PCB+∠PBC=60°,
∴∠BPC=180°-60°=120°,
∵∠CPD=180°-∠BPC=60°,PD=PC,
∴△CDP是等边三角形,
∴CD=CP,∠DCP=∠ACB=60°,
∴∠DCA=∠PCB,
∴△DCA≌△PCB(SAS),
∴AD=PB,
∴BD=PB+PD=AD+DC;
(2)如图,作CM⊥BD于M,AN⊥BD于N.
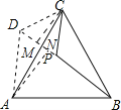
∵△DCA≌△PCB,
∴∠ADC=∠BPC=120°,
∴∠ADP=60°,
∴CM=CDsin60°,AN=ADsin60°,
∴S四边形ABCD=S△BDC+S△BDA
=![]() BDCM+
BDCM+![]() BDAN
BDAN
=![]() BDsin60°(CD+AD)
BDsin60°(CD+AD)
=![]() ×2×
×2×![]() ×2=
×2=![]() .
.

【题目】为了解居民用水情况,小明在某小区随机抽查了20户家庭的月用水量,结果如下表:
月用水量(m3) | 4 | 5 | 6 | 8 | 9 |
户数 | 4 | 5 | 7 | 3 | 1 |
则关于这20户家庭的月用水量,下列说法错误的是( )
A.中位数是6m![]() B.平均数是5.8m
B.平均数是5.8m![]()
C.众数是6m![]() D.极差是6m
D.极差是6m![]()
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?