题目内容
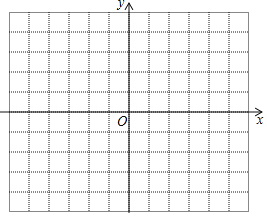
【题目】如图，已知二次函数 
的图像过点A(-4，3），B(4，4).
（1）求抛物线二次函数的解析式.
（2）求一次函数直线AB的解析式．
（3）看图直接写出一次函数直线AB的函数值大于二次函数的函数值的x的取值范围．
（4）求证：△ACB是直角三角形．
【答案】（1）
；（2）
；（3）﹣4﹤x﹤4；（4）见解析
【解析】
（1）由题意把A点或B点坐标代入得到
，即可得出抛物线二次函数的解析式；
（2）根据题意把A点或B点坐标代入y=kx+b，利用待定系数法即可求出一次函数直线AB的解析式；
（3）由题意观察函数图像，根据y轴方向直线在曲线上方时，进而得出x的取值范围；
（4）根据题意求出C点坐标，进而由两点的距离公式或者是构造直角三角形进行分析求证即可.
解：(1)把A点或B点坐标代入得到，
∴抛物线二次函数的解析式为：
.
（2）把A点或B点坐标代入y=kx+b列出方程组
，解得
，
得出一次函数直线AB的解析式为：..
（3）由图象可以看出：一次函数直线AB的函数值大于二次函数的函数值的x的取值范围为：﹣4﹤x﹤4.
（4）由抛物线的表达式得：C点坐标为（-2，0），
由两点的距离公式或者是构造直角三角形得出，
，
，
．
∴
，
∴△ACB是直角三角形.
练习册系列答案
相关题目
【题目】根据学习函数的经验，探究函数y＝x2+ax﹣4|x+b|+4（b＜0）的图象和性质：
（1）下表给出了部分x，y的取值；
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知，a＝ ，b＝ ；
（2）用你喜欢的方式在坐标系中画出函数y＝x2+ax﹣4|x+b|+4的图象；
（3）结合你所画的函数图象，写出该函数的一条性质；
（4）若方程x2+ax﹣4|x+b|+4＝x+m至少有3个不同的实数解，请直接写出m的取值范围．
