题目内容
【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题: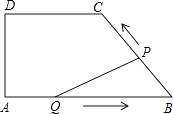
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
【答案】
(1)
解:作CE⊥AB于E,
∵DC∥AB,DA⊥AB,
∴四边形AECD是矩形,
∴AE=CD=5,CE=AD=4,
∴BE=3,
∴BC= ![]() ,
,
∴BC<AB,
∴P到C时,P、Q同时停止运动,
∴t= ![]() (秒),
(秒),
即t=5秒时,P,Q两点同时停止运动
(2)
解:由题意知,AQ=BP=t,
∴QB=8﹣t,
作PF⊥QB于F,则△BPF~△BCE,
∴ ![]() ,即
,即 ![]() ,
,
∴BF= ![]() ,
,
∴S= ![]() QBPF=
QBPF= ![]() ×
× ![]() (8﹣t)=
(8﹣t)= ![]() =﹣
=﹣ ![]() (t﹣4)2+
(t﹣4)2+ ![]() (0<t≤5),
(0<t≤5),
∵﹣ ![]() <0,
<0,
∴S有最大值,当t=4时,S的最大值是 ![]()
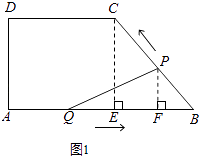
(3)
解:∵cos∠B= ![]() ,
,
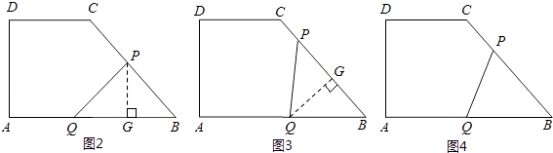
① 当PQ=PB时(如图2所示),则BG= ![]() BQ,
BQ, ![]() =
= ![]() =
= ![]() ,解得t=
,解得t= ![]() s,
s,
②当PQ=BQ时(如图3所示),则BG= ![]() PB,
PB, ![]() =
= ![]() =
= ![]() ,解得t=
,解得t= ![]() s,
s,
③当BP=BQ时(如图4所示),则8﹣t=t,
解得:t=4.
综上所述:当t= ![]() s,
s, ![]() s或t=4s时,△PQB为等腰三角形
s或t=4s时,△PQB为等腰三角形
【解析】(1)通过比较线段AB,BC的大小,找出较短的线段,根据速度公式可以直接求得;(2)由已知条件,把△PQB的边QB用含t的代数式表示出来,三角形的高可由相似三角形的性质也用含t的代数式表示出来,代入三角形的面积公式可得到一个二次函数,即可求出S的最值;(3)根据等腰三角形的性质和余弦公式列出等式求解,即可求的结论.
【考点精析】利用相似三角形的应用对题目进行判断即可得到答案,需要熟知测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.

 备战中考寒假系列答案
备战中考寒假系列答案