题目内容
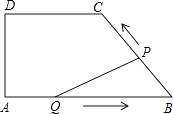
【题目】课外兴趣小组活动时,老师出示了如下问题:如图①,已知在四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,求证:AB+AD=![]() AC.
AC.
小敏反复探索,不得其解.她想,可先将四边形ABCD特殊化,再进一步解决该问题.
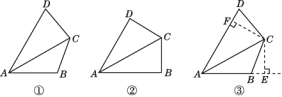
(1)由特殊情况入手,添加条件:“∠B=∠D”,如图②,可证AB+AD=![]() AC.请你完成此证明.
AC.请你完成此证明.
(2)受到(1)的启发,在原问题中,添加辅助线:过C点分别作AB,AD的垂线,垂足分别为点E,F,如图③.请你补全证明过程.
【答案】(1)见解析;(2)见解析.
【解析】
(1)如果:“∠B=∠D”,根据∠B与∠D互补,那么∠B=∠D=90°,又因为∠DAC=∠BAC=30°,因此我们可在直角三角形ADC和ABC中得出AD=AB=![]() AC,那么AD+AB=
AC,那么AD+AB=![]() AC.
AC.
(2)按(1)的思路,作好辅助线后,我们只要证明三角形CFD和BCD全等即可得到(1)的条件.根据AAS可证两三角形全等,DF=BE.然后按照(1)的解法进行计算即可.
(1)证明:∵∠B=∠D=90°,
AC平分∠DAB,
∠DAB=60°,∴CD=CB,
∠CAB=∠CAD=30°.
设CD=CB=x,则AC=2x.
由勾股定理,得AD=![]() CD=
CD=![]() x,AB=
x,AB=![]() CB=
CB=![]() x.
x.
∴AD+AB=![]() x+
x+![]() x=2
x=2![]() x=
x=![]() AC,即AB+AD=
AC,即AB+AD=![]() AC.
AC.
(2)解:由(1)知,AE+AF=![]() AC.
AC.
∵AC为角平分线,CF⊥AD,CE⊥AB,
∴CF=CE,∠CFD=∠CEB=90°.
∵∠ABC与∠D互补,
∠ABC与∠CBE也互补,
∴∠D=∠CBE,
∴△CDF≌△CBE(AAS).
∴DF=BE.∴AB+AD=AB+(AF+FD)=(AB+BE)+AF=AE+AF=![]() AC.
AC.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案【题目】甲、乙、丙三人到文具店购买同一种笔记本和钢笔,甲、乙两人购买的数量及总价分别如表:
甲 | 乙 | |
笔记本(本) | 20 | 15 |
钢笔(支) | 12 | 25 |
总价(元) | 312 | 330 |
(1)求笔记本和钢笔的单价;
(2)丙购买24本笔记本和若干支钢笔共花去526元,甲发现丙的总价算错了,请通过计算加以说明.
【题目】某厂计划每天生产零件![]() 个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)由表可知该厂星期四生产零件 个,这周实际生产零件 个.(用含![]() 的代数式表示)
的代数式表示)
(2) 产量最高日比最低日多生产零件 个.
(3) 若该周厂计划每天生产零件数是![]() ,每个零件应支付工资
,每个零件应支付工资![]() 元,且每天超计划数的零件每个另奖
元,且每天超计划数的零件每个另奖![]() 元,那这周实际应支付工资多少元?
元,那这周实际应支付工资多少元?
【题目】校田园科技社团计划购进A,B两种花卉,两次购买每种花卉的数量以及每次的总费用如下表所示:
花卉数量(单位:株) | 总费用 (单位:元) | ||
A | B | ||
第一次购买 | 10 | 25 | 225 |
第二次购买 | 20 | 15 | 275 |
(1)你从表格中获取了什么信息?______________________________(请用自己的语言描述,写出一条即可);
(2)A,B两种花卉每株的价格各是多少元?