题目内容
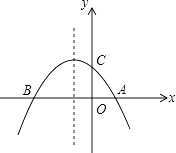
【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号) 
【答案】解:在Rt△CDA中,∠ACD=30°,CD=3000米, ∴AD=CDtan∠ACD=1000 ![]() 米,
米,
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000 ![]() 米,
米,
∴AB=BD﹣AD=2000 ![]() 米.
米.
答:此时渔政船和渔船相距2000 ![]() 米
米
【解析】在Rt△CDB中求出BD,在Rt△CDA中求出AD,继而可得AB,也即此时渔政船和渔船的距离.
【考点精析】掌握关于仰角俯角问题是解答本题的根本,需要知道仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
【题目】某厂计划每天生产零件![]() 个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)由表可知该厂星期四生产零件 个,这周实际生产零件 个.(用含![]() 的代数式表示)
的代数式表示)
(2) 产量最高日比最低日多生产零件 个.
(3) 若该周厂计划每天生产零件数是![]() ,每个零件应支付工资
,每个零件应支付工资![]() 元,且每天超计划数的零件每个另奖
元,且每天超计划数的零件每个另奖![]() 元,那这周实际应支付工资多少元?
元,那这周实际应支付工资多少元?