题目内容
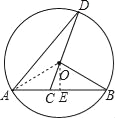
【题目】如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)AB=_____;
(2)当∠D=20°时,求∠BOD的度数.
(3)若△ACD与△BCO相似,求AC的长.

【答案】(1)2![]() ;(2)100°;(3)
;(2)100°;(3)![]() .
.
【解析】试题分析:(1)过点O作OE⊥AB于E,由垂径定理即可求得AB的长;
(2)连接OA,由OA=OB,OA=OD,可得∠BAO=∠B,∠DAO=∠D,则可求得∠DAB的度数,又由圆周角等于同弧所对圆心角的一半,即可求得∠DOB的度数;
(3)由∠BCO=∠A+∠D,可得要使△ACD与△BCO相似,只能∠DCA=∠BCO=90°,然后由相似三角形的性质即可求得答案.
试题解析:解:(1)过点O作OE⊥AB于E,则AE=BE=![]() AB,∠OEB=90°.∵OB=2,∠B=30°,∴BE=OBcos∠B=2×
AB,∠OEB=90°.∵OB=2,∠B=30°,∴BE=OBcos∠B=2×![]() =
=![]() ,∴AB=
,∴AB=![]() .故答案为:
.故答案为: ![]() .
.
(2)连接OA.∵OA=OB,OA= OD,∴∠BAO=∠B,∠DAO=∠D,∴∠DAB=∠BAO+∠DAO=∠B+∠D.又∵∠B=30°,∠D=20°,∴∠DAB=50°,∴∠BOD=2∠DAB=100°;
(3)∵∠BCO=∠A+∠D,∴∠BCO>∠A,∠BCO>∠D,∴要使△ACD与△BCO相似,只能∠DCA=∠BCO=90°,此时∠BOC=60°,∠BOD=120°,∴∠DAC=60°,∴△DAC∽△BOC.∵∠BCO=90°,即OC⊥AB,∴AC= ![]() AB=
AB=![]() ,∴若△ACD与△BCO相似,AC的长度为
,∴若△ACD与△BCO相似,AC的长度为![]() .
.

练习册系列答案
相关题目





