题目内容
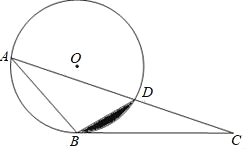
【题目】已知![]() 是
是![]() 的一条弦,点
的一条弦,点![]() 在
在![]() 上,联结
上,联结![]() 并延长,交弦
并延长,交弦![]() 于点
于点![]() ,且
,且![]() .
.
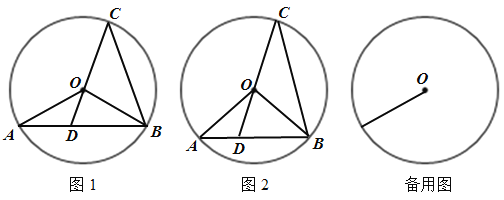
(1)如图1,如果![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(2)如图2,如果![]() ,求
,求![]() 的值;
的值;
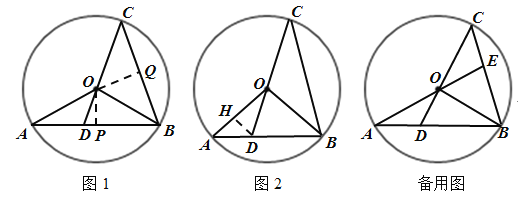
(3)延长线段![]() 交弦
交弦![]() 于点
于点![]() ,如果
,如果![]() 是等腰三角形,且
是等腰三角形,且![]() 的半径长等于
的半径长等于![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() (3)
(3)![]() 和
和![]()
【解析】
(1)由题意利用弦心距即可求证结果,
(2)此题关键先求出AO,做辅助线构造特殊三角形,并求证出∠AOD,再根据平行线分线段成比例求出比值即可,
(3)分情况讨论两种情况:OE=BE时或OB=BE时两种情况,利用三角形相似即△COE![]() △CBO找到相似比,利用相似比求解即可.
△CBO找到相似比,利用相似比求解即可.
(1)过点O作OP⊥AB,垂足为点P;OQ⊥BC,垂足为点Q,
∵BO平分∠ABC,
∴OP=OQ,
∵OP,OQ分别是弦AB、BC 的弦心距,
∴AB= BC;
(2)∵OA=OB,
∴∠A=∠OBD,
∵CD=CB,
∴∠CDB =∠CBD,
∴∠A+∠AOD =∠CBO +∠OBD,
∴∠AOD =∠CBO,
∵OC=OB,
∴∠C =∠CBO,
∴∠DOB =∠C +∠CBO = 2∠CBO = 2∠AOD,
∵AO⊥OB,
∴∠ AOB =∠AOD +∠BOD =3∠AOD = 90°,
∴∠AOD=30°,
过点D作DH⊥AO,垂足为点H,
∴∠AHD=∠DHO=90°,
∴tan∠AOD =![]() =
=![]() ,
,
∵∠AHD=∠AOB=90°,
∴HD‖OB,
∴![]() ,
,
∵OA=OB,
∴HD=AH,
∵HD‖OB,
∴![]() ;
;
(3)∵∠C=∠CBO,
∴∠OEB =∠C+∠COE >∠CBO,
∴OE≠OB;
若OB = EB =2时,
∵∠C=∠C,∠COE =∠AOD =∠CBO,
∴△COE![]() △CBO,
△CBO,
∴![]() ,
,
∴![]() ,
,
∴![]() -2BC -4=0,
-2BC -4=0,
∴BC =![]() +1 (舍去)或BC =
+1 (舍去)或BC =![]() +1,
+1,
∴BC =![]() +1;
+1;
若OE = EB时,
∵∠EOB =∠CBO,
∵∠OEB =∠C+∠COE =2∠C =2∠CBO且∠OEB +∠CBO +∠EOB = 180°,
∴4∠CBO=180°,∠CBO=45°,
∴∠OEB=90°,
∴cos∠CBO=![]() ,
,
∵OB=2,
∴EB =![]() ,
,
∵OE过圆心,OE⊥BC,
∴BC =2EB =2![]() .
.

 阅读快车系列答案
阅读快车系列答案