题目内容
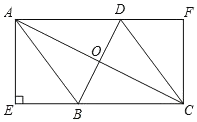
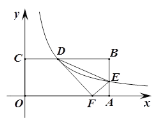
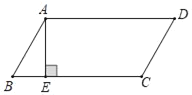
【题目】如图,在ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为_____
【答案】2cm或4cm或10cm
【解析】
由三角函数得出BE=2,分两种情况:
①当∠PAD=90°时,点P与E重合,BP=BE=2;
②当∠APD=90°时,作DF⊥ABC于F,则∠DFP=∠AEP=90°,DF=AE=4,证明△APE∽△PDF,得出![]() ,解得PE=2,或PE=8,得出BP=BE+PE=4,或BP=BE+PE=10;即可得出答案.
,解得PE=2,或PE=8,得出BP=BE+PE=4,或BP=BE+PE=10;即可得出答案.
解:∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∵tanB=![]() =2,且AE=4,
=2,且AE=4,
∴BE=2,
分两种情况:
①当∠PAD=90°时,点P与E重合,BP=BE=2;
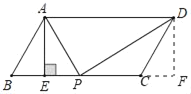
②当∠APD=90°时,作DF⊥ABC于F,如图所示:
则∠DFP=∠AEP=90°,DF=AE=4,
∵∠APE+∠PAE=∠APE+∠DPF=90°,
∴∠PAE=∠DPF,
∴△APE∽△PDF,
∴![]() ,即
,即![]() =
=![]() ,
,
解得:PE=2,或PE=8,
∴BP═BE+PE=4,或BP=BE+PE=10
综上所述,若△PAD为直角三角形,则BP的长为2cm或4cm或10cm;
故答案为:2cm或4cm或10cm.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目