题目内容
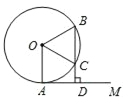
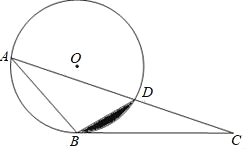
【题目】如图,△ABC中,⊙O经过A、B两点,且交AC于点D,连接BD,∠DBC=∠BAC.
(1)证明BC与⊙O相切;
(2)若⊙O的半径为6,∠BAC=30°,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)6π-9![]() .
.
【解析】
(1)连接BO并延长交⊙O于点E,连接DE.由圆周角定理得出∠BDE=90°,再求出∠EBD+∠DBC=90°,根据切线的判定定理即可得出BC是⊙O的切线;
(2)分别求出等边三角形DOB的面积和扇形DOB的面积,即可求出答案.
(1)证明:连接BO并延长交⊙O于点E,连接DE,
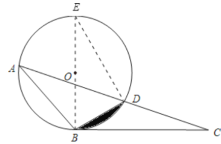
∵BE是直径,∴∠EDB=90°,
∴∠E+∠EBD=90°
∵![]() =
=![]() ,∴∠E=∠A
,∴∠E=∠A
又∵∠DBC=∠BAC,∴∠DBC=∠E
∴∠DBC+∠EBD=90°,∴∠EBC=90°,∴BC⊥EB.
又∵OB是半径(B在⊙O上),∴BC与⊙O相切.
(2)∵![]() =
=![]() ,∴∠BOD=2∠A=60°
,∴∠BOD=2∠A=60°
S阴影= S扇形OBD-S△OBD=π36×![]() -9
-9![]() =6π-9
=6π-9![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目