Question

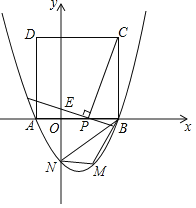
【题目】如果一个四边形有且只有三个顶点在圆上，那么称这个四边形是该圆的“联络四边形”，已知圆的半径长为，这个圆的一个联络四边形是边长为的菱形，那么这个菱形不在圆上的顶点与圆心的距离是________．

Answer 1

【答案】1

【解析】

此题应根据题意先找到圆心位置，再根据圆心位置求出不在圆上的顶点到该圆圆心的距离即可．

根据题意作图可分两种情况：1如图：作， BC=，BO=5，

∵A，B，C在圆O上，

∴BP=（垂径定理），

又，

∴OP== =；

因为ABCD是菱形，

∴ACBD，即∠BQC=90°，

在△BOP与△BQC中，

，

∴△BOP△BQC，

∴，

即，

∴BQ=2，

∵BQ>BO，

∴此情况不符合题意，舍去；

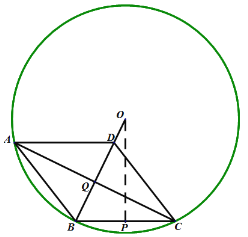
2，如图，同理可得OP=，

在△BOP与△BQC中，

，

∴△BOP△BQC，

∴ ，

即，

∴BQ=2，

∴OQ=BO-BQ=3，

∴OD== =1，

综上所述，这个菱形不在圆上的顶点与圆心的距离是1．

故答案是：1．