Question

【题目】在△ABC中，AB＝AC，CD是AB边上的中线，点E在边AC上（不与A，C重合），且BE＝CD．设＝k，若符合条件的点E有两个，则k的取值范围是_____．

Answer 1

【答案】且

【解析】

符合条件的点E有两个E、E1，则AC边上的高垂直平分EE1，由等腰三角形的性质得出BE是中线，AE=CE，求出当CD⊥AB时，BE⊥AC，满足条件的点E有一个，此时△ABC是等边三角形，AB=BC，=1；求出当满足条件的一个点E1与点A重合时，=；当满足条件的一个点E1与点C重合时，BE=BC，证明△BCE∽△ABC，得出=，求出AB=BC，得出=,即可得出结果．

解：设=k，若符合条件的点E有两个E、E1，

则AC边上的高垂直平分EE1，

∵AB=AC，CD是AB边上的中线，BE=CD，

∴BE是中线，AE=CE，

当CD⊥AB时，BE⊥AC，满足条件的点E有一个，

此时△ABC是等边三角形，AB=BC，

=1；

当满足条件的一个点E1与点A重合时，BE=AB，

作BG⊥AC于G，如下图所示：

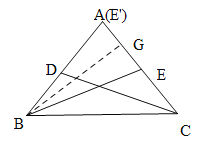
则AG=EG=AE=AC=AB，

由勾股定理得：BG2=AB2-AG2，

BC2=BG2+CG2=AB2-AG2+CG2=AB2-（AB）2+（AB）2=AB2，

∴BC=AB，

∴=；

当满足条件的一个点E1与点C重合时，BE=BC，

如下图所示：

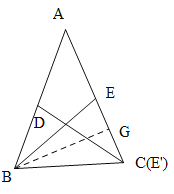
∴∠BCE=∠BEC，

∵AB=AC，

∴∠ABC=∠ACB，

∴∠BCE=∠BEC=∠ABC=∠ACB，

∴△BCE∽△ABC，

∴=，

∴BC2=AB×CE=AB2，

∴AB=BC，

∴=；

综上所述，设=k，若符合条件的点E有两个，则k的取值范围是：＜k＜，且k≠1；

故答案为＜k＜，且k≠1．