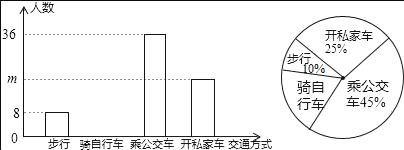
题目内容
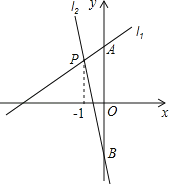
【题目】如图,直线l1与l2相交于点P,点P横坐标为﹣1,l1的解析式为y=![]() x+3,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
x+3,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
(1)求点B的坐标;
(2)求直线l2的解析式;
(3)若点M为直线l2上一动点,直接写出使△MAB的面积是△PAB的面积的![]() 的点M的坐标;
的点M的坐标;
(4)当x为何值时,l1,l2表示的两个函数的函数值都大于0?
【答案】(1)(0,﹣3);(2)y=﹣![]() x﹣3;(3)M点的坐标是(﹣
x﹣3;(3)M点的坐标是(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() );(4)﹣6<x<﹣
);(4)﹣6<x<﹣![]()
【解析】
(1)先利用l1的解析式求出点A的坐标,再根据A、B关于x轴对称,横坐标不变,纵坐标互为相反数解答;
(2)根据点P的横坐标是﹣1,求出点P的坐标,然后利用待定系数法列式求解即可;
(3)根据三角形的面积,底边AB不变,只要点M的横坐标的绝对值等于点P的横坐标的长度的![]() 求出点M的横坐标,然后代入直线l2的解析式求解即可;
求出点M的横坐标,然后代入直线l2的解析式求解即可;
(4)分别求出两直线解析式与x轴的交点坐标,根据x轴上方的部分的函数值大于0解答.
解:(1)l1:y=![]() x+3,当x=0时,
x+3,当x=0时,![]() x+3=0+3=3,
x+3=0+3=3,
∴点A的坐标是(0,3),
∵点A与点B恰好关于x轴对称,
∴B点坐标为(0,﹣3);
(2)∵点P横坐标为﹣1,且点P在l1上,
∴![]() ×(﹣1)+3=
×(﹣1)+3=![]() ,
,
∴点P的坐标是(﹣1,![]() ),
),
设直线l2的解析式为y=kx+b,
则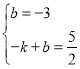 ,解得
,解得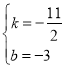 ,
,
∴直线l2的解析式为y=﹣![]() x﹣3;
x﹣3;
(3)∵点P横坐标是﹣1,△MAB的面积是△PAB的面积的![]() ,
,
∴点M的横坐标的绝对值是![]() ,
,
①当横坐标是﹣![]() 时,y=(﹣
时,y=(﹣![]() )×(﹣
)×(﹣![]() )﹣3=
)﹣3=![]() ﹣3=﹣
﹣3=﹣![]() ,
,
②当横坐标是![]() 时,y=(﹣
时,y=(﹣![]() )×
)×![]() ﹣3=﹣
﹣3=﹣![]() ﹣3=﹣
﹣3=﹣![]() ,
,
∴M点的坐标是(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() );
);
(4)l1:y=![]() x+3,当y=0时,
x+3,当y=0时,![]() x+3=0,解得x=﹣6,
x+3=0,解得x=﹣6,
l2:y=﹣![]() x﹣3,当y=0时,﹣
x﹣3,当y=0时,﹣![]() x﹣3=0,
x﹣3=0,
解得x=﹣![]() ,
,
∴当﹣6<x<﹣![]() 时,l1、l2表示的两个函数的函数值都大于0.
时,l1、l2表示的两个函数的函数值都大于0.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案