题目内容
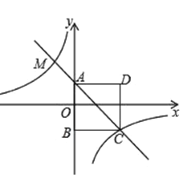
【题目】矩形OABC的边OA、OC分别在y轴和x轴的正半轴上，且长分别为m、4m，D为AB的中点，抛物线y＝﹣x2+bx+c经过点A、点D．
（1）当m＝1时，求抛物线y＝﹣x2+bx+c的函数关系式；
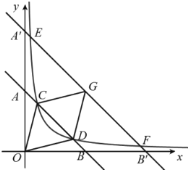
（2）延长BC至点E，连接OE，若OD平分∠AOE，抛物线与线段CE相交，求抛物线的顶点P到达最高位置时的坐标．
【答案】（1）抛物线解析式为：y＝﹣x2+2x+1；（2）此时抛物线l顶点P到达最高位置时的坐标为（
，
）．
【解析】
(1)由m＝1，得：点A（0，1），点C（4，0），点B（4，1），点D（2，1），根据待定系数法，即可得到答案；
(2)由待定系数法得：抛物线的解析式为y＝﹣x2+2mx+m，过点D作DA'⊥OE，交x轴于点Q，过点A′作A′N⊥x轴于点N，连接AA'，求出A′点坐标为（
m，﹣
m），进而得到：直线OA′的解析式为：y＝﹣
x，从而得到点E的坐标和抛物线l与直线CE的交点坐标，根据抛物线l与线段CE相交，求出
≤m≤
，进而求出抛物线顶点P到达最高位置时的坐标.
（1）如图1，
∵m＝1，
∴点A（0，1），点C（4，0），点B（4，1），
∵D为AB的中点，
∴点D（2，1）
∵抛物线y＝﹣x2+bx+c经过点A、点D，
∴
，解得：
∴抛物线解析式为：y＝﹣x2+2x+1；
（2）∵点A（0，m），点C（4m，0），点B（4m，m），
∵D为AB的中点，
∴点D（2m，m）
∵抛物线y＝﹣x2+bx+c经过点A、点D，
∴
，解得：
，
∴抛物线的解析式为y＝﹣x2+2mx+m，
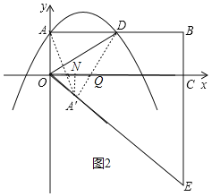
如图2，过点D作DA'⊥OE，交x轴于点Q，过点A′作A′N⊥x轴于点N，连接AA'，
∵OD平分∠AOE，
∴∠AOD＝∠A'OD，
又∵∠OAD＝∠OA′D＝90°，OD＝OD，
∴△AOD≌△A'OD（AAS）
∴OA＝OA′＝m，AD＝A′D＝2m，∠ADO＝∠A′DO，
∵矩形OABC中，AD∥OC，
∴∠ADO＝∠DOQ，
∴∠A′DO＝∠DOQ，
∴DQ＝OQ．
设DQ＝OQ＝x，则A′Q＝2m﹣x，
在Rt△OA′Q中，∵OA′2+A′Q2＝OQ2，
∴m2+（2m﹣x）2＝x2，
解得：x＝
m．
∵S△OA′Q＝OQA′N＝OA′A′Q，
∴A′N＝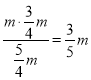
，
∴ON＝
，
∴A′点坐标为（m，﹣m），
∴直线OA′的解析式为：y＝﹣x，
当x＝4m时，y＝﹣×4m＝﹣3m，
∴E点坐标为（4m，﹣3m）．
当x＝4m时，﹣x2+2mx+m＝﹣（4m）2+2m4m+m＝﹣8m2+m，
即抛物线l与直线CE的交点坐标为：（4m，﹣8m2+m），
∵抛物线l与线段CE相交，
∴﹣3m≤﹣8m2+m≤0，
∵m＞0，
∴﹣3≤﹣8m+1≤0，
解得：≤m≤；
∵y＝﹣x2+2mx+m＝﹣（x﹣m）2+m2+m，且≤m≤，
∴当x＝m时，y有最大值m2+m，
又∵m2+m＝（m+）2﹣
，
∴当≤m≤时，m2+m随m的增大而增大，
∴当m＝时，顶点P到达最高位置，即：m2+m＝（
）2+＝，
故抛物线l顶点P到达最高位置时的坐标为（，）．
