Question

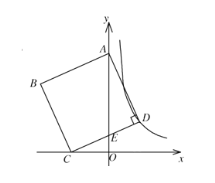
【题目】如图，AB是⊙O的直径，点D，C在⊙O上，∠DOC＝90°，AD＝，BC＝1，则⊙O的半径为（　　）

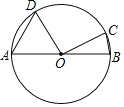
A.B.C.D.

Answer 1

【答案】C

【解析】

如图延长DO交⊙O于E，作EF⊥CB交CB的延长线于F，连接BE、EC．只要证明△EFB是等腰直角三角形，即可推出EF＝BF＝1，再利用勾股定理求出EC即可解决问题

解：如图延长DO交⊙O于E，作EF⊥CB交CB的延长线于F，连接BE、EC．

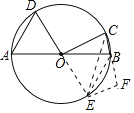
∵∠AOD＝∠BOE，

∴，

∴AD＝BE＝，

∵∠DOC＝∠COE＝90°，OC＝OB＝OE，

∴∠OCB＝∠OBC，∠OBE＝∠OEB，

∴∠CBE＝（360°﹣90°）＝135°，

∴∠EBF＝45°，

∴△EBF是等腰直角三角形，

∴EF＝BF＝1，

在Rt△ECF中，EC＝＝，

∵△OCE是等腰直角三角形，

∴OC＝．

故选：C．